题目内容
在△ABC中,∠C=90°,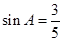 ,那么
,那么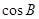 的值等于( )
的值等于( )
A.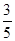 B.
B.  C.
C.  D.
D. 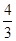
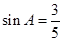 ,那么
,那么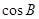 的值等于( )
的值等于( )A.
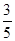 B.
B.  C.
C.  D.
D. 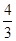
A
根据∠A+∠B=90°得出cosB=sinA,代入求出即可.
解:
∵∠C=90°,sinA=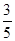 ,
,
又∵∠A+∠B=90°,
∴cosB=sinA=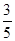 .
.
故选A.
本题考查了对互余两角三角函数的关系的应用,注意:已知∠A+∠B=90°,能推出sinA=cosB,cosA=sinB,tanA=cotB,cotA=tanB.
解:

∵∠C=90°,sinA=
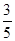 ,
,又∵∠A+∠B=90°,
∴cosB=sinA=
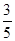 .
.故选A.
本题考查了对互余两角三角函数的关系的应用,注意:已知∠A+∠B=90°,能推出sinA=cosB,cosA=sinB,tanA=cotB,cotA=tanB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =1.732)
=1.732)



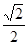
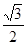

 │+(
│+( -cosB)
-cosB) =0,则∠C=_______度.
=0,则∠C=_______度.
