题目内容
试求|x-1|+|x-3|+…+|x-2003|+|x-2005|的最小值．
解：∵2005=2×1003-1，
∴共有1003个数，
∴x=502×2-1=1003时，两边的数关于|x-1003|对称，此时的和最小，
此时|x-1|+|x-3|+…+|x-2003|+|x-2005|
=（x-1）+（x-3）…+（1001-x）+（1003-x）+（1005-x）+…+（2005-x）
=2（2+4+6+…+1002）
=2×
=503004．
故答案为：503004．
分析：根据绝对值的性质，两端的数距离远点越近，则所求的值越小，然后进行解答即可．
点评：本题考查了绝对值的性质，判断出当x=1003时，代数式的和最小是解题的关键．
∴共有1003个数，
∴x=502×2-1=1003时，两边的数关于|x-1003|对称，此时的和最小，
此时|x-1|+|x-3|+…+|x-2003|+|x-2005|
=（x-1）+（x-3）…+（1001-x）+（1003-x）+（1005-x）+…+（2005-x）
=2（2+4+6+…+1002）
=2×
=503004．
故答案为：503004．
分析：根据绝对值的性质，两端的数距离远点越近，则所求的值越小，然后进行解答即可．
点评：本题考查了绝对值的性质，判断出当x=1003时，代数式的和最小是解题的关键．
练习册系列答案
相关题目
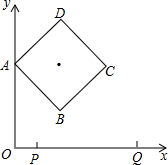1个单位长度的速度从点P（1，0）出发沿x轴向终点Q（7，0）匀速运动，设两点运动的时间为t秒．