Question

【题目】如图，四边形中，，是上一点，且、分别平分、.

(1)求证：；

(2)若，，求四边形的面积.

Answer 1

【答案】（1）见解析；（2）12.

【解析】

（1）延长AE，BC交于M，根据AE、BE分别平分∠BAD、∠ABC，可得出∠AEB=90°，利用ASA证明△ABE≌△MBE，得出AE=ME后，再证明△ADE≌△MCE，即可得出结论．

（2）根据S四边形ABCD=S△ABM=2S△ABE，即可得出答案．

(1)如图，延长AE，BC交于M，

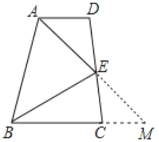
∵AD∥BC，

∴∠DAB+∠ABC=180，

又∵AE、BE分别平分∠BAD、∠ABC，

∴∠DAE=∠EAB，∠ABE=∠MBE，

∴∠EAB+∠ABE==90，

∴∠BEA=∠BEM=90゜，

在△ABE和△MBE中,

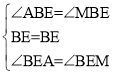
∴△ABE≌△MBE（ASA），

∴AE=ME，

∵AD∥BC

∴∠D=∠ECM

在△ADE和△MCE中,

∴△ADE≌△MCE（AAS），

∴CE=DE.

(2)S△ABE=AE·BE=6，

∵△ADE≌△MCE，AE=ME，

∴S四边形ABCD=S△ABM=2S△ABE=12.