题目内容
如图所示,点M是矩形ABCD的边AD的中点,点P是BC边上的一动点,PE⊥MC,PF⊥MB,垂足为E,F.
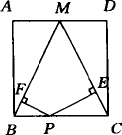
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明;
(2)在(1)中,当P运动到什么位置时,矩形PEMF变为正方形,为什么?
答案:
解析:
解析:
|
证明:(1)当AD=2AB时,四边形PEMF为矩形. ∵AD=2AB,而AM=DM.∴△AMB为等腰直角三角形, 同理,△CDM为等腰直角三角形,∴∠AMB=∠DMC=45°, ∴∠BMC=90°. 又∠MFP=∠MEP=90°,∴四边形PEMF为矩形. (2)当点P位于BC中点时,矩形PEMF为正方形. ∵△BMC为等腰直角三角形,当点P位于BC的中点时,矩形PEMF为正方形. ∵△BMC为等腰三角形,当点P位于BC中点时,有PE=PF,故矩形PEMF为正方形. |

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
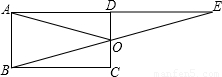
 (2013•邵阳)如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论不正确的是( )
(2013•邵阳)如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论不正确的是( )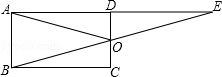
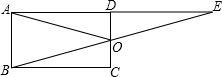 如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论不正确的是
如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,连结AO,下列结论不正确的是