题目内容
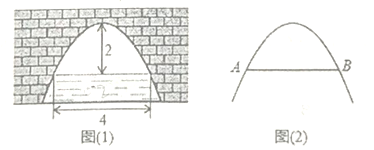
【题目】如图（1）是一个横断面为抛物线形状的拱桥，当水面宽
为
时，拱顶与水面距离为
.
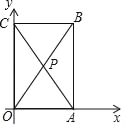
（1）请你在图（2）中，建立适当的平面直角坐标系，使该抛物线拱桥的函数关系式符合
形式，并求此时，函数关系式；
（2）当水面上升
时，求水面宽度.
【答案】（1）
；（2）
.
【解析】
（1）以抛物线的顶点为坐标原点，线段
的中垂线为
轴建立坐标系，再利用待定系数法求得函数解析式；
（2）求出（1）中所求函数解析式
时
的值，据此可得.
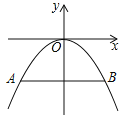
（1）建立平面直角坐标系，则通过画图可得知
为原点，
抛物线以轴为对称轴，且经过
、
两点，抛物线顶点坐标为
，
通过以上条件可设顶点式
，其中
可通过代入点坐标
，
到抛物线解析式得出：
，
所以抛物线解析式为
；
（2）
水面上升
m，
，
故
，
解得：
，
，
则水面的宽为
（
）.
答：水面宽度为.
练习册系列答案
相关题目
