题目内容
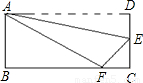
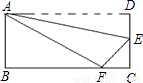
 如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于
如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于
- A.1
- B.2
- C.3
- D.4
B
分析:由四边形ABCD是矩形与AB=6,△ABF的面积是24,易求得BF的长,然后由勾股定理,求得AF的长,根据折叠的性质,即可求得AD,BC的长,继而求得答案.
解答:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,
∵AB=6,
∴S△ABF= AB•BF=
AB•BF= ×6×BF=24,
×6×BF=24,
∴BF=8,
∴AF= =
= =10,
=10,
由折叠的性质:AD=AF=10,
∴BC=AD=10,
∴FC=BC-BF=10-8=2.
故选B.
点评:此题考查了矩形的性质、直角三角形的性质、勾股定理以及折叠的性质.此题难度适中,注意掌握数形结合思想的应用,注意折叠中的对应关系.
分析:由四边形ABCD是矩形与AB=6,△ABF的面积是24,易求得BF的长,然后由勾股定理,求得AF的长,根据折叠的性质,即可求得AD,BC的长,继而求得答案.
解答:∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,
∵AB=6,
∴S△ABF=
 AB•BF=
AB•BF= ×6×BF=24,
×6×BF=24,∴BF=8,
∴AF=
 =
= =10,
=10,由折叠的性质:AD=AF=10,
∴BC=AD=10,
∴FC=BC-BF=10-8=2.
故选B.
点评:此题考查了矩形的性质、直角三角形的性质、勾股定理以及折叠的性质.此题难度适中,注意掌握数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 (2012•黔东南州)如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )
(2012•黔东南州)如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )