题目内容
已知△ABC的面积为8cm2,连接△ABC各边中点构成第一个三角形,再连接这个新三角形的各边中点得到第2个三角形.依此类推,则第100个三角形的面积为
- A.

- B.

- C.

- D.

C
分析:由△ABC的面积为8cm2,连接△ABC各边中点构成第一个三角形,根据三角形的中位线的性质与相似三角形的判定定理,即可得第一个三角形与△ABC相似,且相似比为:1:2,然后由相似三角形面积比等于相似比的平方,可得面积比为:1:4,则可求得第一个三角形的面积,以此类推,的规律:第n个三角形的面积为 ;继而可求得答案.
;继而可求得答案.
解答:∵连接△ABC各边中点构成第一个三角形,
∴第一个三角形与△ABC相似,且相似比为:1:2,
∴面积比为:1:4,
∵△ABC的面积为8cm2,
∴第一个三角形的面积为:8× =2;
=2;
同理:第二个三角形的面积为:(8× )×
)× =
= ;
;
∴第n个三角形的面积为:8×( )n=
)n= =
= ;
;
∴第100个三角形的面积为: =
= .
.
故选C.
点评:此题考查了相似三角形的判定与性质以及三角形中位线的性质.此题那难度适中,注意得到规律:第n个三角形的面积为 是关键.
是关键.
分析:由△ABC的面积为8cm2,连接△ABC各边中点构成第一个三角形,根据三角形的中位线的性质与相似三角形的判定定理,即可得第一个三角形与△ABC相似,且相似比为:1:2,然后由相似三角形面积比等于相似比的平方,可得面积比为:1:4,则可求得第一个三角形的面积,以此类推,的规律:第n个三角形的面积为
 ;继而可求得答案.
;继而可求得答案.解答:∵连接△ABC各边中点构成第一个三角形,
∴第一个三角形与△ABC相似,且相似比为:1:2,
∴面积比为:1:4,
∵△ABC的面积为8cm2,
∴第一个三角形的面积为:8×
 =2;
=2;同理:第二个三角形的面积为:(8×
 )×
)× =
= ;
;∴第n个三角形的面积为:8×(
 )n=
)n= =
= ;
;∴第100个三角形的面积为:
 =
= .
.故选C.
点评:此题考查了相似三角形的判定与性质以及三角形中位线的性质.此题那难度适中,注意得到规律:第n个三角形的面积为
 是关键.
是关键. 
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
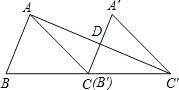 已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( )
已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为( ) 25、如图,已知△ABC的面积为3,且AE=AC,现将△ABC沿CA方向平移CA长度得到△EFA,求四边形CEFB的面积.
25、如图,已知△ABC的面积为3,且AE=AC,现将△ABC沿CA方向平移CA长度得到△EFA,求四边形CEFB的面积.