题目内容
如图,已知抛物线 ,直线
,直线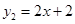 ,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
下列给出四个说法:
①当x>0时,y1<y2;
②当x<0时,x值越大,M值越大;
③使得M大于2的x值不存在;
④使得M=1的x值是 或
或 .
.
说法正确的个数是
| A.1个 | B.2个 | C.3个 | D.4个 |
B.
解析试题分析:∵当y1=y2时,即-2x2+2=2x+2时,
解得:x=0或x=-1,
∴当x<-1时,利用函数图象可以得出y2>y1;当-1<x<0时,y1>y2;当x>0时,利用函数图象可以得出y2>y1;
∴①错误;
∵抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴②错误;
∵抛物线y1=-2x2+2,直线y2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y1=-2x2+2,最大值为2,故M大于2的x值不存在;
∴使得M大于2的x值不存在,
∴③正确;由图可知,x=0时,M有最大值为2,故①正确;
抛物线与x轴的交点为(-1,0)(1,0),
由图可知,-1<x<0时,M=2x+2,
当M=1时,2x+2=1,
解得x=- ,
,
x>0时,M=-2x2+2,
当M=1时,-2x2+2=1,
解得x=- ,
,
所以,使得M=1的x值是? 或
或 ,故④正确,
,故④正确,
综上所述,③④都正确.
故选B.
考点:二次函数的性质;一次函数的性质.

某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )
A. | B. | C. | D. |
如图,点A的坐标为(6,0),点B为y轴的负半轴上的一个动点,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度为( )
| A.2 | B.3 |
| C.4 | D.PB的长度随点B的运动而变化 |
如图,以两条直线l1,l2的交点坐标为解的方程组是
A. | B. | C. | D. |
如图,一次函数y=(m﹣2)x﹣1的图象经过二、三、四象限,则m的取值范围是( )
| A.m>0&nbs, | B.m<0&nbs, | C.m>2&nbs, | D.m<2&nbs, |





 (千米)与时间
(千米)与时间 (小时)的函数关系的大致图象是( )
(小时)的函数关系的大致图象是( )



 ,则a的值是( )
,则a的值是( )




