题目内容
2.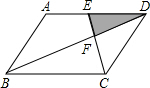 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )| A. | 8S | B. | 9S | C. | 10S | D. | 11S |
分析 由于四边形ABCD是平行四边形,那么AD∥BC,AD=BC,根据平行线分线段成比例定理的推论可得△DEF∽△BCF,再根据E是AD中点,易求出相似比,从而可求△BCF的面积,再利用△BCF与△DEF是同高的三角形,则两个三角形面积比等于它们的底之比,从而易求△DCF的面积,进而可求?ABCD的面积.
解答 解:如图所示,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴S△DEF:S△BCF=($\frac{DE}{BC}$)2,
又∵E是AD中点,
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴DE:BC=DF:BF=1:2,
∴S△DEF:S△BCF=1:4,
∴S△BCF=4S,
又∵DF:BF=1:2,
∴S△DCF=2S,
∴S?ABCD=2(S△DCF+S△BCF)=12S.
∴四边形ABCE的面积=9S,
故选B.
点评 本题考查了平行四边形的性质、平行线分线段成比例定理的推论、相似三角形的判定和性质.解题的关键是知道相似三角形的面积比等于相似比的平方、同高两个三角形面积比等于底之比,先求出△BCF的面积.

练习册系列答案
相关题目
12.不等式4x-8≤0的解集是( )
| A. | x≥-2 | B. | ≤-2 | C. | ≥2 | D. | ≤2 |
13.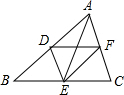 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )| A. | ∠BAC=90° | B. | BC=2AE | C. | DE平分∠AEB | D. | AE⊥BC |
10.下列说法中正确的是( )
| A. | 了解一批日光灯的使用寿命适宜采用抽样调查 | |
| B. | “打开电视,正在播放《沈视早报》”是必然事件 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 一组数据的波动越大,方差越小 |
17.2017年1月25日,摩拜单车正式进入济南市场,第一批共投放了11000辆单车,11000用科学记数法表示为( )
| A. | 1.1×103 | B. | 1.1×104 | C. | 11×103 | D. | 0.11×105 |
7.函数y=$\frac{1}{\sqrt{x-1}}$中,自变量x的取值范围是( )
| A. | x≥1 | B. | x>1 | C. | x<1 | D. | x≤1 |
14.下列计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | (x-y)2=x2-2xy-y2 | C. | x(x-1)=x2-1 | D. | (x+1)(x-1)=x2-1 |
11. 如图是一个正方体,则它的表面展开图可以是( )
如图是一个正方体,则它的表面展开图可以是( )
 如图是一个正方体,则它的表面展开图可以是( )
如图是一个正方体,则它的表面展开图可以是( )| A. |  | B. |  | C. |  | D. |  |