Question

【题目】两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连接ME，MC．试判断△EMC的形状，并说明理由．

Answer 1

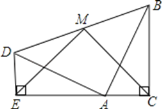
【答案】△EMC是等腰直角三角形，证明见解析

【解析】

欲判断△EMC的形状，需知道其三边关系．根据题意需证EM＝CM，由此证明△EMD≌△CMA即可．依据等腰直角三角形性质易证．

解：△EMC是等腰直角三角形．

理由如下：

连接MA．

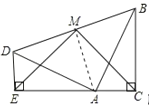
∵∠EAD＝30°，∠BAC＝60°，∴∠DAB＝90°，

∵△EDA≌△CAB，∴DA＝AB，ED＝AC，

∴△DAB是等腰直角三角形．

∴∠MDA＝∠MBA＝45°

又∵M为BD的中点，

∴∠MAD＝∠MAB＝45°，AM⊥BD（三线合一），

∴AM＝=MD，

∴∠EDM＝∠MAC＝105°，

在△MDE和△MAC中，

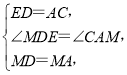
∴△MDE≌△MAC．

∴∠DME＝∠AMC，ME＝MC，

又∵∠DMA＝90°，∴∠EMC＝∠EMA+∠AMC＝∠EMA+∠DME＝∠DMA＝90°．

∴△MEC是等腰直角三角形．