Question

如图，平面直角坐标系中，⊙O的圆心O为坐标原点，半径为1．长始终为的线段PQ的一个端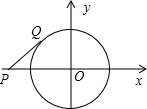点Q在⊙O上运动，另一个端点P也随之在x轴的负半轴上移动．在运动过程中：
（1）当线段PQ所在的直线与⊙O相切时，求P点的坐标；
（2）当∠OPQ最大时，求直线PQ的解析式；
（3）当∠OPQ=30°时，求Q点的坐标．

Answer 1

解：（本题12分）
（1）当线段PQ所在的直线与⊙O相切时，连接OQ，则OQ⊥QP，
在Rt△OPQ中，PQ=，OQ=1，则OP=，
所以点P（-，0）；

（2）当∠OPQ最大时，点Q运动到⊙O与y轴交点，
在Rt△OPQ中，PQ=，OQ=1，则OP=1，
所以点P（-1，0），点Q（0，1）或（0，-1），
所以直线PQ的解析式为y=x+1或y=-x-1；

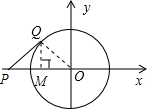
（3）当∠OPQ=30°时，连接OQ，作QM⊥OP于点M，
在Rt△QPM中，PQ=，∠OPQ=30°，则QM=，
在Rt△QOM中，OM=，
所以点Q₁（-，）；Q₂（-，）；Q₃（，）；Q₄（，-）．
分析：（1）依题意，连接OQ，则OQ⊥QP．利用勾股定理求出OP，继而可求出点P的坐标；
（2）当∠OPQ最大时，点Q运动到⊙O与y轴交点，利用勾股定理求出OP的值继而求出坐标P，Q．然后可求出直线PQ的解析式；
（3）依题意连接OQ，作QM⊥OP．在Rt△QPM中，PQ=，∠OPQ=30°，可求出QM的值，又因为在Rt△QOM中OM=，可求出点Q的坐标．
点评：本题综合的是切线的性质以及一次函数的综合运用，难度中等．