Question

（2012•大港区一模）如图，在平面直角坐标系中，点C的坐标为（0，4），A是x轴正半轴上的一个动点，M是线段AC的中点．把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB．过B作x轴的垂线、过C作y轴的垂线，两直线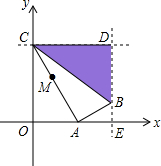交于D，直线DB交x轴于一点E．
（1）求证：△AOC∽△BEA；
（2）如果点A的横坐标为t，△BCD的面积为S，当t为何值时，S=6.25？
（3）如果以B、C、D为顶点的三角形与△AOC相似，求此时点A的坐标．

Answer 1

分析：（1）由题意可得：∠CAB=90°，∠COA=∠BEA=90°，又由同角的余角相等，即可求得∠BAE=∠OCA，然后根据有两角对应相等的三角形相似，即可判定△AOC∽△BEA；
（2）由△AOC∽△BEA，根据相似三角形的对应边成比例，即可求得AE与BE的长，继而求得S与t的关系，又由S=6.25，即可求得t的值；
（3）由∠BDC=∠AOC=90°，可分别从当

CD

OC

=

DB

OA

，即

t+2

4

=

4- 1 2 t

t

时，△BDC∽△AOC与当

BD

OC

=

CD

OA

，即

4- 1 2 t

4

=

t+2

t

时，△BDC∽△COA去分析求解即可求得答案．

解答：（1）证明：∵由题意得：∠CAB=90°，
∴∠OAC+∠BAE=90°，
又∵OC⊥OA，
∴∠OCA+∠OAC=90°，
∴∠BAE=∠OCA，
又∵∠COA=∠BEA=90°，
∴△OCA∽△EAB；

（2）∵△OCA∽△EAB，
∴

OC

AE

=

OA

BE

=

AC

AB

=

2

1

，
∴

4

AE

=

t

BE

=

2

1

，
∴AE=2，BE=

1

2

t，
∴CD=OE=OA+AE=t+2，DE=OC-BE=4-

1

2

t，
∴S=

1

2

CD•BD=

1

2

（t+2）（4-

1

2

t）=-

1

4

t²+

3

2

t+4，
∴S=-

1

4

t²+

3

2

t+4=6.25，
二次项系数化1，得：t²-6t+9=0，
解得：t₁=t₂=3，
∴当t=3时，S=6.25；

（3）∵∠BDC=∠AOC=90°，
∴当

CD

OC

=

DB

OA

，即 

t+2

4

=

4- 1 2 t

t

时，△BDC∽△AOC，
解得：t₁=2

5

-2，t₂=-2

5

-2（舍去）；
当 

BD

OC

=

CD

OA

，即 

4- 1 2 t

4

=

t+2

t

时，△BDC∽△COA，
整理，得：t²=-16（无实根）；
故A点的坐标为（2

5

-2，0）．

点评：此题考查了相似三角形的判定与性质、旋转的性质以及直角三角形的性质．此题难度较大，注意掌握数形结合思想、分类讨论思想与方程思想的应用．