Question

（本小题满分14分）

如图①，已知四边形ABCD是正方形，点E是AB的中点，点F在边CB的延长线上，且BE=BF，连接EF．

1.（1）若取AE的中点P，求证：BP=CF；

2.（2）在图①中，若将绕点B顺时针方向旋转（0⁰<<360⁰），如图②，是否存在某位置，使得？，若存在，求出所有可能的旋转角的大小；若不存在，请说明理由；

3.（3）在图①中，若将△BEF绕点B顺时针旋转（0⁰<<90⁰），如图③，取AE的中点P，连接BP、CF，求证：BP=CF且BP⊥CF．

 

Answer 1

 

1.解：（1）∵ AE = BE，AP = EP

∴ BE =2PE，AB = 4PE，BP = 3PE…………（1分）

∵ AB =BC，BE =BF      ∴ BC = 4PE，BF = 2PE

∴ CF =6PE…………（2分）        ∴

2.（2）存在…………（４分）

因为将绕点B顺时针方向旋转一周，E、F分别在以点B为圆心，BE为半径的圆周上，如图1，因此过Ａ点做圆Ｂ的切线，设切点是点Ｅ，此时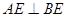，有AE∥BF。

当圆Ｂ的切线ＡＥ在ＡＢ的右侧时，如图1

∵ AE∥BF∴ ∠AEB = ∠EBF= 90°     ∵ BE = AB∴ ∠BAE = 30°

∴ ∠ABE = 60°，即旋转角是60°…………（6分）

当圆Ｂ的切线ＡＥ在ＡＢ的左侧时，如图2

如图2，∵ AE∥BF

∴ ∠AEB + ∠EBF = 180°∴ ∠AEB = 90°

∵ BE = AB     ∴ ∠BAE = 30°

∴ ∠ABE = 60°，即旋转角是300°

3.（3）延长BP到点G，使BP=PG，连结AG

∴ △APG ≌ △BPE

∴ AG =BE，PG = BP，∠G = ∠PBE

∵ BE =BF　　　∴ AG = BF

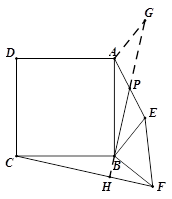∵ △BEF绕点B顺时针旋转   ∴ ∠ABE = ，∠CBF = 180°－

∵ ∠G = ∠PBE　　　　∴ ∠G + ∠ABP=

∴ ∠GAB = 180°－　　　∴ ∠GAB = ∠CBF

又∵ AB =BC，AG = BF

∴ △GAB ≌ △FBC　　　　∴BG = CF

∵ 　　　　∴ …………（11分）

延长PB，与CF相交于点H

∵ △GAB ≌ △FBC　　　　∴ ∠ABP = ∠BCH

∵ ∠ABP + ∠CBH = 90°　　　∴ ∠BCH + ∠CBH=90°

∴ BH⊥CF　　　　即 BP⊥CF…………（14分）

解析:略