题目内容
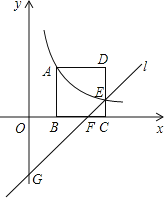
【题目】如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2![]() ,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
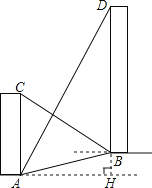
【答案】12![]() 米
米
【解析】
试题分析:作BE⊥AC于E,设BH=x米,则AE=x米,BE=AH=2![]() x米.CE=2
x米.CE=2![]() x
x![]()
![]() 米=2x米,所以AC=3x米,根据5x﹣3x=12求出x的值,近而求出AH的值.
米=2x米,所以AC=3x米,根据5x﹣3x=12求出x的值,近而求出AH的值.
解:作BE⊥AC于E,设BH=x米,
则AE=x米,BE=AH=2![]() x米.CE=2
x米.CE=2![]() x
x![]()
![]() 米=2x米,所以AC=3x米,
米=2x米,所以AC=3x米,
DH=2![]() x
x![]()
![]() 米=6x米,所以BD=5x米,
米=6x米,所以BD=5x米,
5x﹣3x=12,
得x=6,
所以AH=6×2![]() =12
=12![]() (米),
(米),
答:两楼之间水平距离12![]() 米.
米.

练习册系列答案
相关题目