题目内容
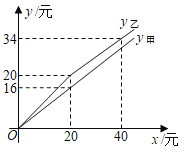
【题目】春季正是新鲜草莓上市的季节,甲、乙两家水果店,平时以同样的价格出售品质相同的草莓,“草莓节”期间,甲、乙两家商店都让利酬宾,顾客的折后付款金额![]() 、
、![]() (单位:元)与标价应付款金额x(单位:元)之间的函数关系如图所示.
(单位:元)与标价应付款金额x(单位:元)之间的函数关系如图所示.
(1)求![]() 、
、![]() 关于x的函数关系式;
关于x的函数关系式;
(2)“草莓节”期间,如何选择甲、乙两家水果店购买草莓更省钱?
【答案】(1)![]() =0.8x;
=0.8x;![]() =
=![]() ;(2)当购买金额按原价小于60元时,到甲商店购买更省钱;当购买金额按原价大于60元时,到乙商店购买更省钱;当购买金额按原价等于60元时,到甲、乙两商店购买花钱一样.
;(2)当购买金额按原价小于60元时,到甲商店购买更省钱;当购买金额按原价大于60元时,到乙商店购买更省钱;当购买金额按原价等于60元时,到甲、乙两商店购买花钱一样.
【解析】
(1)利用待定系数法即可求出y甲,y乙关于x的函数关系式;
(2)当0<x<20时,显然到甲商店购买更省钱;当x≥20时,分三种情况进行讨论即可.
(1)设y甲=kx,把(20,16)代入,
得20k=16,解得k=0.8,
所以y甲=0.8x;
当0<x<20时,设y乙=ax,
把(20,20)代入,得20a=20,解得a=1,
所以y乙=x;
当x≥20时,设y乙=mx+n,
把(20,20),(40,34)代入,得
![]() ,
,
解得![]() ,
,
所以y乙=![]() ;
;
(2)当0<x<20时,0.8x<x,到甲商店购买更省钱;
当x≥20时,若到甲商店购买更省钱,则0.8x<0.7x+6,解得x<60;
若到乙商店购买更省钱,则0.8x>0.7x+6,解得x>60;
若到甲、乙两商店购买一样省钱,则0.8x=0.7x+6,解得x=60;
故当购买金额按原价小于60元时,到甲商店购买更省钱;
当购买金额按原价大于60元时,到乙商店购买更省钱;
当购买金额按原价等于60元时,到甲、乙两商店购买花钱一样.

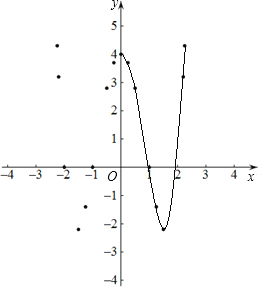
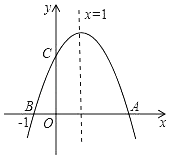
【题目】小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
![]() 自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x |
|
|
|
|
|
|
|
|
| 0 |
|
| 1 |
|
| 2 |
|
|
|
y |
|
|
| 0 |
|
| 0 |
|
| 4 |
|
| 0 |
|
| m |
|
|
|
其中![]() _______;
_______;
![]() 如图,在平面直角坐标系xOy中,把该函数的图象补充完整;
如图,在平面直角坐标系xOy中,把该函数的图象补充完整;
![]() 观察函数图象,写出一条该函数的性质______;
观察函数图象,写出一条该函数的性质______;
![]() 进一步探究函数图象发现:
进一步探究函数图象发现:
![]() 方程
方程![]() 有______个互不相等的实数根;
有______个互不相等的实数根;
![]() 有两个点
有两个点![]() 和
和![]() 在此函数图象上,当
在此函数图象上,当![]() 时,比较
时,比较![]() 和
和![]() 的大小关系为:
的大小关系为:![]() ______
______![]() 填“
填“![]() ”、“
”、“![]() ”或“
”或“![]() ”
”![]() ;
;
![]() 若关于x的方程
若关于x的方程![]() 有4个互不相等的实数根,则a的取值范围是______.
有4个互不相等的实数根,则a的取值范围是______.