题目内容
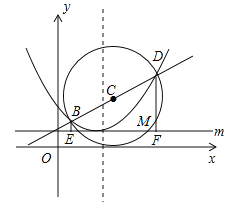
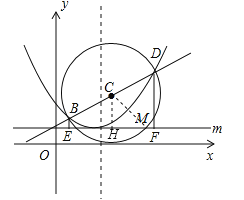
【题目】如图,已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线
(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线![]() 与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求MF的值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)可设抛物线的顶点式,再结合抛物线过点(4,2),可求得抛物线的解析式;
(2)联立直线和抛物线解析式可求得B、D两点的坐标,则可求得C点坐标和线段BD的长,可求得圆的半径,可证得结论;
(3)过点C作CH⊥m于点H,连接CM,可求得MH,利用(2)中所求B、D的坐标可求得FH,则可求得MF和BE的长,可求得其比值.
试题解析:
(1)∵已知抛物线![]() (a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为
(a≠0)的图象的顶点坐标是(2,1),∴可设抛物线解析式为![]() ,∵抛物线经过点(4,2),∴
,∵抛物线经过点(4,2),∴![]() ,解得a=
,解得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,即
,即![]() ;
;
(2)联立直线和抛物线解析式可得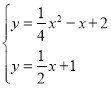 ,解得:
,解得: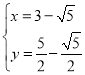 或
或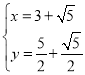 ,∴B(
,∴B(![]() ,
,![]() ),D(
),D(![]() ,
,![]() ),∵C为BD的中点,∴点C的纵坐标为
),∵C为BD的中点,∴点C的纵坐标为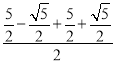 =
=![]() ,∵BD=
,∵BD=![]() =5,∴圆的半径为
=5,∴圆的半径为![]() ,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
,∴点C到x轴的距离等于圆的半径,∴圆C与x轴相切;
(3)如图,过点C作CH⊥m,垂足为H,连接CM,由(2)可知CM=![]() ,CH=
,CH=![]() ﹣1=
﹣1=![]() ,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=
,在Rt△CMH中,由勾股定理可求得MH=2,∵HF=![]() =
=![]() ,∴MF=HF﹣MH=
,∴MF=HF﹣MH=![]() ,∵BE=
,∵BE=![]() ﹣1=
﹣1=![]() ,∴
,∴![]() =
=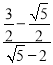 =
=![]() .
.

练习册系列答案
相关题目