题目内容
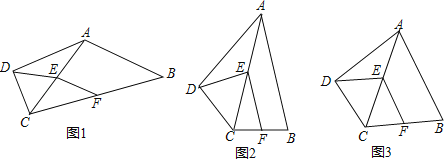
【题目】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF、DE.
(1)请在图1中找出长度相等的两条线段?并说明理由.(AB=AC除外)
(2)如图2,当AC平分∠BAD,∠DEF=90°时,求∠BAD的度数.
(3)如图3,四边形CDEF是边长为2的菱形,求S四边形ABCD.
【答案】(1)DE=EF,见解析;(2)∠BAD=60°;(3)S四边形ABCD=6![]() .
.
【解析】
(1)利用直角三角形斜边的中线性质和三角形的中位线性质可得结论;
(2)先证明∠CEF=![]() ∠BAD,∠DEC=∠BAD,根据∠DEF=90°列方程得∠BAD的度数;
∠BAD,∠DEC=∠BAD,根据∠DEF=90°列方程得∠BAD的度数;
(3)由四边形CDEF是菱形,说明△CDE是等边三角形,再根据等底同高说明△CDE与△DEA间关系,根据相似说明△CAB与△CEF间关系,由DE=2得AB=4,得等边△DEC的面积,利用三角形的面积间关系得结论.
(1)DE=EF,
在△ABC中,点E,F分别为AC,BC的中点,
∴EF∥AB,且EF=![]() AB,
AB,
在Rt△ACD中,点E为AC的中点,
∴DE=![]() AC,
AC,
∵AB=AC,
∴DE=EF;
(2)∵AC平分∠BAD,EF∥AB,
DE=![]() AC=AE=EC,
AC=AE=EC,
∴∠BAC=∠DAC,∠CEF=∠BAC,∠DEC=2∠DAC=∠BAD,
∵∠DEF=90°,
∴∠CEF+∠DEC=∠BAC+2∠DAC=90°,
∴∠BAC=∠DAC=30°,
∴∠BAD=60°;
(3)四边形ABCD的面积为:
∵四边形CDEF是菱形,EC=DE,
∴△CDE与△CEF都是等边三角形,
∵EF=DE=CD=CF=2,
∴AB=4,
∴S△DCE=S△DEA=S△CEF![]() ;
;
∵EF∥AB,
∴![]() ,
,
∴S△ABC=4S△CEF=4![]()
∴S四边形ABCD=S△DCE+S△DEA+S△ABC=2×![]() +4
+4![]() =6
=6![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试. 现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
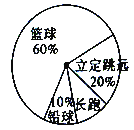
项目选择统计图
训练后篮球定时定点投篮测试进球统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是___________,该班共有同学___________人;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%. 请求出参加训练之前的人均进球数.