题目内容
设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1、y2、y3的大小关系为()
| A.y1>y2>y3 | B.y1>y3>y2 | C.y3>y2>y1 | D.y3>y1>y2 |
A
解析试题分析:由题意抛物线开口向下,则距离抛物线的对称轴距离越远的点的纵坐标越小.
∵抛物线y=-(x+1)2+a的开口向下,对称轴为x=-1
且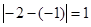 ,
,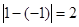 ,
,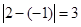
∴y1>y2>y3
故选A.
考点:二次函数的性质
点评:二次函数的性质是初中数学的重点,是中考必考题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
|
线路 |
绕路 |
直路 |
|
路程 |
300公里 |
180公里 |
|
过路费 |
30元 |
90元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为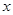 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.
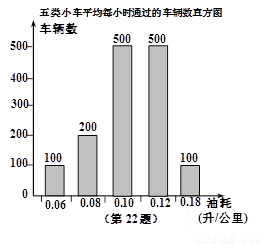
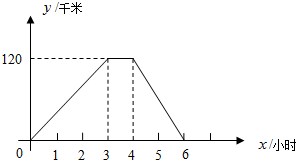 距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题:
距甲地的距离为y米,y与x的函数图象如图所示.根据图象信息,解答下列问题: