Question

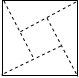如图是2002年北京第24届国际数学家大会会标，它由4个全等的直角三角形拼合而成，若图中大、小正方形的面积分别为13和1，则直角三角形的较长直角边长为

 

．

Answer 1

分析：根据图中大、小正方形的面积可以计算大、小正方形的边长，找到两直角边相差1，两直角边平方和等于斜边的平方的等量关系，从而求解．

解答：解：设图中直角三角形的边长分别为a、b，
∵图中大、小正方形的面积为13和1，则大、小正方形的边长为

13

、1，
则a、b满足a-b=1，a²+b²=(

13

)2，
解得a=3、b=2，
故较长的直角边为3，
故答案为 3．

点评：本题考查了直角三角形中勾股定理的运用，本题中找到a-b=1和a²+b²=(

13

)2的等量关系是解题的关键．