Question

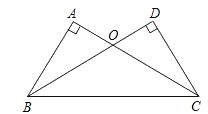
【题目】如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD，AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′；

（1）求证：△ABD≌△ACD′；

（2）若∠BAC=120°，求∠DAE的度数．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据对称得出AD=AD′，根据SSS证△ABD≌△ACD′即可；

（2）根据全等得出∠BAD=∠CAD′，求出∠BAC=∠DAD′，根据对称得出∠DAE=∠DAD′，代入求出即可．

（）证明：∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，

∴，

在△ABD和△ACD′中，

∵ ，

∴ △ABD≌△ACD′（SSS）.

（）解：∵≌，

∴，

∴，

∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，

∴，

即．