题目内容
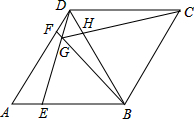 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H. (1)求证:△AED≌△DFB;
(2)求证:∠DEB=∠CBG;
(3)求证:S四边形BCDG=
| ||
| 4 |
考点:四边形综合题
专题:
分析:(1)根据已知可知△ABD为等边三角形,再根据SAS即可证△AED≌△DFB;
(2)根据∠DEB外角性质,∠DEB=∠A+∠ADE,又∠CBG=∠DBC+∠DBF,容易得到∠A=∠DBC,∠ADE=∠DBF,即可证
(3)先求证点B、C、D、G四点共圆,根据圆周角性质,得出∠BGC=∠DGC=60°,容易求证△CBM≌△CDN,S四边形BCDG=S四边形CMGN=2S△CMG,根据有一个角为60°的特殊直角三角形性质,求得两直角边,即可证
(2)根据∠DEB外角性质,∠DEB=∠A+∠ADE,又∠CBG=∠DBC+∠DBF,容易得到∠A=∠DBC,∠ADE=∠DBF,即可证
(3)先求证点B、C、D、G四点共圆,根据圆周角性质,得出∠BGC=∠DGC=60°,容易求证△CBM≌△CDN,S四边形BCDG=S四边形CMGN=2S△CMG,根据有一个角为60°的特殊直角三角形性质,求得两直角边,即可证
解答:证明:(1)∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS);
(2)∵ABCD为菱形,△ABD为等边三角形
∴∠A=∠DBC=60°,
由(1)已证△AED≌△DFB,
∴∠ADE=∠DBF,
∵∠DEB=∠A+∠ADE,∠CBG=∠DBC+∠DBF,
∴∠DEB=∠CBG;
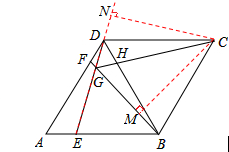
(3)∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(HL)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
CG,CM=
CG,
∴S四边形CMGN=2S△CMG=2×
×GM×CM=2×
×
CG×
CG=
CG2;
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS);
(2)∵ABCD为菱形,△ABD为等边三角形
∴∠A=∠DBC=60°,
由(1)已证△AED≌△DFB,
∴∠ADE=∠DBF,
∵∠DEB=∠A+∠ADE,∠CBG=∠DBC+∠DBF,
∴∠DEB=∠CBG;

(3)∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(HL)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
| 1 |
| 2 |
| ||
| 2 |
∴S四边形CMGN=2S△CMG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:考查三角形全等的求证,巧妙地把四边形与圆的知识结合,难度有点大,综合性强

练习册系列答案
相关题目
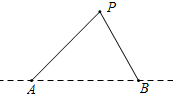 国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?
国外船只,除特许外,不得进入我国海洋100海里以内区域.如图,设A,B是我们观察站A和B之间为150海里,海岸线是过A,B的一条直线,一外国船只在P点,在A点测到∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告?