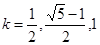题目内容
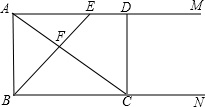
如图,射线BN、AM都垂直于线段AB,E为AM上一动点,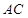 ⊥
⊥ 于F,交BN于C,
于F,交BN于C, ⊥
⊥ 于
于 ,连接BD.
,连接BD.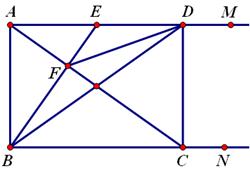
⑴求证: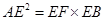 ;
;
⑵当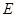 为
为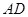 的中点时,求证:
的中点时,求证:  ;
;
⑶设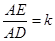 ,请探究出使
,请探究出使 为
为
等腰三角形的实数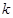 的值.
的值.
⑴4分,证明略.
⑵4分,由⑴有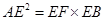 ,因为
,因为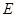 为
为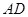 的中点,所以
的中点,所以 ,则
,则 ,又因为
,又因为 ,所以
,所以 ,则
,则 .
.
⑶4分. ,(
,( 同样算对)
同样算对)
探究出一个解,得1分;探究出两个解共得2分;探究出三个解共得4分;
以下解法供参考
要使 为等腰三角形,分三种情况讨论,
为等腰三角形,分三种情况讨论,
① 为腰,且
为腰,且 为顶角顶点;
为顶角顶点;
② 为腰,且
为腰,且 为顶角顶点;
为顶角顶点;
③ 为底.
为底.
① 为腰,且
为腰,且 为顶角顶点;
为顶角顶点;
由⑵当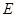 为
为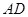 的中点时,可知
的中点时,可知 ,又易知四边形
,又易知四边形 为矩形,所以
为矩形,所以 ,又易知
,又易知 ,所以
,所以 ;又由四边形
;又由四边形 为矩形可知,
为矩形可知, ,所以
,所以 ,从而
,从而 ,于是
,于是 ,则
,则 为等腰三角形,此时
为等腰三角形,此时 ;
;
② 为腰,且
为腰,且 为顶角顶点;
为顶角顶点;
此时, ,容易得到
,容易得到 ,则点
,则点 为
为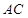 黄金分割点,
黄金分割点, ;
;
③ 为底.
为底.
此时, ,容易得到
,容易得到 ,不难得到四边形
,不难得到四边形 为正方形,
为正方形,
解析

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,射线AM∥BN,∠A=∠B=90°,点D、C分别在AM、BN上运动(点D不与A重合、点C不与B重合),E是AB边上的动点(点E不与A、B重合),在运动过程中始终保持DE⊥EC且AD+DE=AB=a.
如图,射线AM∥BN,∠A=∠B=90°,点D、C分别在AM、BN上运动(点D不与A重合、点C不与B重合),E是AB边上的动点(点E不与A、B重合),在运动过程中始终保持DE⊥EC且AD+DE=AB=a.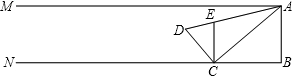
 ⊥
⊥ 于F,交BN于C,
于F,交BN于C, ⊥
⊥ 于
于 ,连接BD.
,连接BD.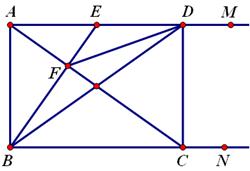
 ;
; 为
为 的中点时,求证:
的中点时,求证:  ;
;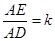 ,请探究出使
,请探究出使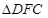 为
为 的值.
的值. 

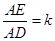 ,当使
,当使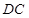 为腰,且
为腰,且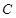 为顶角顶点;
为顶角顶点;