题目内容
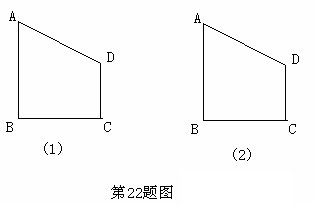
已知ABCD在平面直角坐标系中的位置如图所示,抛物线y=ax2+bx-5经过A、B、C三点且交CD 于F,线段AD所在直线的函数解析式为y=-3x+3.
于F,线段AD所在直线的函数解析式为y=-3x+3.
①求点A、D的坐标;
②若ABCD的面积为12,求抛物线的函数解析式;
③在②的条件下,请问抛物线上是否存在点P,使得以CD、CP为邻边的平行四边形的面积是ABCD面积的 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
解:①线段AD所在直线的函数解析式为y=-3x+3,
令y=0,得x=1,
∴A点坐标为(1,0),
令x=0,得y=3,
∴D点坐标为(0,3).
②设B点坐标为B(x,0),
AB=x-1,
又∵四边形ABCD的面积为12,
AB•OD=12,即(x-1)•3=12,
解得x=5,
∴B(5,0)
将A,B两点代入抛物线的解析式y=ax2+bx-5中,
解得 ,
,
∴抛物线的函数解析式为y=-x2+6x-5
③设抛物线上存在点P使得以CD、CP为邻边的平行四边形的面积是ABCD面积的
设P点坐标为P(x,y),
∵CD=AB=4
∴CD•|y-3|= ×12,即|y-3|=
×12,即|y-3|= ,
,
∴y= 或
或 ,
,
将其代入抛物线的解析式中,
当y= 时,x=
时,x= ,
,
∴点P的坐标为( ,
, )或(
)或( ,
, )
)
当y= 时,x=
时,x=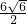 ,
,
∴点P的坐标为( ,
, )或(
)或( ,
, ).
).
分析:①分别令一次函数的解析式中的y=0,和x=0,即可得点A,D的坐标.
②由平行四边形的面积可求出线段AB的长,再加上线段OA的长度,即得B点的横坐标.将A,B两点代入,即得抛物线的解析式.
③可先设出P点的坐标,根据面积可求出P点的纵坐标,然后将其代入抛物线方程中,求出横坐标.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
令y=0,得x=1,
∴A点坐标为(1,0),
令x=0,得y=3,
∴D点坐标为(0,3).
②设B点坐标为B(x,0),
AB=x-1,
又∵四边形ABCD的面积为12,
AB•OD=12,即(x-1)•3=12,
解得x=5,
∴B(5,0)
将A,B两点代入抛物线的解析式y=ax2+bx-5中,
解得
 ,
,∴抛物线的函数解析式为y=-x2+6x-5
③设抛物线上存在点P使得以CD、CP为邻边的平行四边形的面积是ABCD面积的

设P点坐标为P(x,y),
∵CD=AB=4
∴CD•|y-3|=
 ×12,即|y-3|=
×12,即|y-3|= ,
,∴y=
 或
或 ,
,将其代入抛物线的解析式中,
当y=
 时,x=
时,x= ,
,∴点P的坐标为(
 ,
, )或(
)或( ,
, )
)当y=
 时,x=
时,x=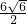 ,
,∴点P的坐标为(
 ,
, )或(
)或( ,
, ).
).分析:①分别令一次函数的解析式中的y=0,和x=0,即可得点A,D的坐标.
②由平行四边形的面积可求出线段AB的长,再加上线段OA的长度,即得B点的横坐标.将A,B两点代入,即得抛物线的解析式.
③可先设出P点的坐标,根据面积可求出P点的纵坐标,然后将其代入抛物线方程中,求出横坐标.
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 与双曲线
与双曲线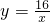 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.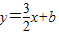 与双曲线
与双曲线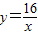 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.