题目内容
△ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是
- A.AB=c,AC=b,BC=a,DE=
 ,EF=
,EF= ,DF=
,DF=
- B.AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1
- C.AB=3,AC=4,BC=6,DE=12,EF=8,DF=6
- D.AB=
 ,AC=
,AC= ,BC=
,BC= ,DE=
,DE= ,EF=3,DF=3
,EF=3,DF=3
C
分析:根据相似三角形的判定定理(有三组对应边的比相等的两个三角形相似)判断即可.
解答:
A、根据AB=c,BC=a,AC=b,de= ,EF=
,EF= ,DF=
,DF= ,不能推出三组对应边的比相等,即这两个三角形不相似,故本选项错误;
,不能推出三组对应边的比相等,即这两个三角形不相似,故本选项错误;
B、∵AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1,
∴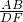 =1,
=1, =
= ,
, =
= ,
,
∴三组对应边的比不相等,即这两个三角形不相似,故本选项错误;
C、∵AB=3,AC=4,BC=6,DE=12,EF=8,DF=6,
∴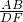 =
= =
= =
= ,
,
∴△ABC和△DEF相似,故本选项正确;
D、∵AB= ,AC=
,AC= ,BC=
,BC= ,DE=
,DE= ,EF=3,DF=3,
,EF=3,DF=3,
∴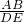 =
=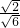 =
= ,
, =
= ,
, =
= ,
,
∴三组对应边的比不相等,即这两个三角形不相似,故本选项错误;
故选C.
点评:本题考查了相似三角形的判定的应用,注意:相似三角形的判定定理之一是:有三组对应边的比相等的两个三角形相似.
分析:根据相似三角形的判定定理(有三组对应边的比相等的两个三角形相似)判断即可.
解答:

A、根据AB=c,BC=a,AC=b,de=
 ,EF=
,EF= ,DF=
,DF= ,不能推出三组对应边的比相等,即这两个三角形不相似,故本选项错误;
,不能推出三组对应边的比相等,即这两个三角形不相似,故本选项错误;B、∵AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1,
∴
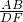 =1,
=1, =
= ,
, =
= ,
,∴三组对应边的比不相等,即这两个三角形不相似,故本选项错误;
C、∵AB=3,AC=4,BC=6,DE=12,EF=8,DF=6,
∴
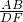 =
= =
= =
= ,
,∴△ABC和△DEF相似,故本选项正确;
D、∵AB=
 ,AC=
,AC= ,BC=
,BC= ,DE=
,DE= ,EF=3,DF=3,
,EF=3,DF=3,∴
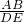 =
=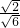 =
= ,
, =
= ,
, =
= ,
,∴三组对应边的比不相等,即这两个三角形不相似,故本选项错误;
故选C.
点评:本题考查了相似三角形的判定的应用,注意:相似三角形的判定定理之一是:有三组对应边的比相等的两个三角形相似.

练习册系列答案
相关题目


