题目内容
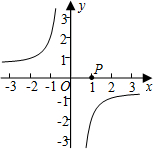 已知点P的坐标为(1,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数
已知点P的坐标为(1,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数 的图象上,则符合条件的点M的坐标为________.
的图象上,则符合条件的点M的坐标为________.
(2,-1)或(-1,2)
分析:设正方形PQMN的边长为s,由P点坐标为(1,0),当M在第四象限,可得点M的坐标为:(1+s,-s),当M在第二象限,点M1的坐标为:(1-s,s),又由点M落在反比例函数y=- 的图象上,即可分别求得点M点的坐标.
的图象上,即可分别求得点M点的坐标.
解答: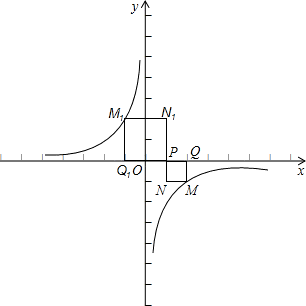 解:设正方形PQMN的边长为s,
解:设正方形PQMN的边长为s,
当M在第四象限,
∵P点坐标为(1,0),
∴点M的坐标为:(1+s,-s),
∵点M落在反比例函数y=- 的图象上,
的图象上,
∴-s=-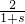 ,
,
解得:s=1或s=-2(不合题意舍去),
∴M的坐标是(2,-1);
当M在第二象限,
∵P点坐标为(1,0),
∴点M1的坐标为:(1-s,s),
∵点M落在反比例函数y=- 的图象上,
的图象上,
∴s=-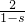 ,
,
解得:s=2或s=-1(不合题意舍去),
∴M的坐标是(-1,2);
故答案为:(2,-1)或(-1,2).
点评:此题主要考查了反比例函数的综合应用,即动点所形成的几何图形在直角坐标系中与反比例函数的应用,是一道函数与几何的综合题,由几何图形中的数量关系建立函数和推理探究等多个知识点,实际上是数形结合思想的运用,融代数与几何为一体,把代数问题与几何问题进行相互转化.
分析:设正方形PQMN的边长为s,由P点坐标为(1,0),当M在第四象限,可得点M的坐标为:(1+s,-s),当M在第二象限,点M1的坐标为:(1-s,s),又由点M落在反比例函数y=-
 的图象上,即可分别求得点M点的坐标.
的图象上,即可分别求得点M点的坐标.解答:
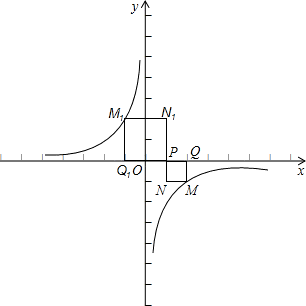 解:设正方形PQMN的边长为s,
解:设正方形PQMN的边长为s,当M在第四象限,
∵P点坐标为(1,0),
∴点M的坐标为:(1+s,-s),
∵点M落在反比例函数y=-
 的图象上,
的图象上,∴-s=-
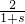 ,
,解得:s=1或s=-2(不合题意舍去),
∴M的坐标是(2,-1);
当M在第二象限,
∵P点坐标为(1,0),
∴点M1的坐标为:(1-s,s),
∵点M落在反比例函数y=-
 的图象上,
的图象上,∴s=-
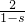 ,
,解得:s=2或s=-1(不合题意舍去),
∴M的坐标是(-1,2);
故答案为:(2,-1)或(-1,2).
点评:此题主要考查了反比例函数的综合应用,即动点所形成的几何图形在直角坐标系中与反比例函数的应用,是一道函数与几何的综合题,由几何图形中的数量关系建立函数和推理探究等多个知识点,实际上是数形结合思想的运用,融代数与几何为一体,把代数问题与几何问题进行相互转化.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
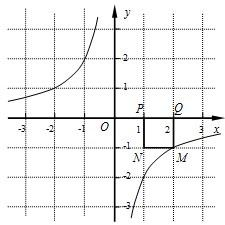 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=- 如图,抛物线y=ax2+bx(a>0)与双曲线y=
如图,抛物线y=ax2+bx(a>0)与双曲线y= (2013•宜宾)如图,直线y=x-1与反比例函数y=
(2013•宜宾)如图,直线y=x-1与反比例函数y=