Question

【题目】如1，在平面直角坐标系中，直线分别与轴、轴交于点，等边的顶点与原点重合，边落在轴正半轴上，点恰好落在线段上，将等边从图1的位置沿轴正方向以每秒1个单位长度的速度平移，边分别与线段交于点(如图2所示)，设平移的时间为(s)．

(1) ，等边的边长为 ；

(2)在运动过程中，当为何值时，MN垂直平分AB；

(3)在开始平移的同时，点从的顶点出发，以每秒2个单位长度的速度沿折线运动，当点运动到时立即停止运动，也随之停止平移．

①当点在线段上运动时，若，求的值；

②当点在线段上运动时，若的面积，求的值．

Answer 1

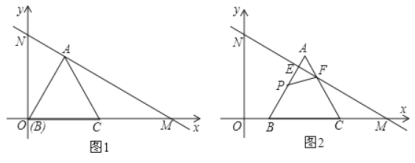
【答案】（1）30°，3；（2）3；（3）①或；②2

【解析】

（1）根据，∠OMN=30°和△ABC为等边三角形，求证△OAM为直角三角形，然后即可得出答案．

（2）易知当点C与M重合时直线MN平分线段AB，此时OB=3，由此即可解决问题；

（3）①分为点P在EF下方和P在EF上方两种情况讨论，分别表示出PE和AE，用AE=2PE，即可解得t值；

②确定好点P的表示，表示出EF，及P到EF的高度，用三角形面积公式，即可解得t值．

（1）∵直线MN分别与x轴正半轴、y轴正半轴交于点M、N，

∴OM=6cm，ON=，

∴tan∠OMN= =，

∴∠OMN=30°，

∴∠ONM=60°，

∵△ABC为等边三角形，

∴∠AOC=60°，∠NOA=30°，

∴OA⊥MN，即△OAM为直角三角形，

∴OA=OM=×6=3．

故答案为30°，3．

（2）若直线MN垂直平分AB，则MN与中过点C的高重合

故当点C与M重合时直线MN平分线段AB，此时，

又右移的速度为每秒1个单位，所以t=3．

故答案为3．

（3）①由题意知BP=2t，BM=6﹣t，

∵∠BEM=90°，∠BME=30°，

∴BE=3﹣，AE=AB﹣BE=，

若P在EF下方

则

∵

∴，即

若P在EF上方，

则

∵

∴，即

故的值为：或

②由BP=2t，BM=6﹣t，

∵∠BEM=90°，∠BME=30°，

∴BE=3﹣，AE=AB﹣BE=，

∵

∴，

∴

∴P到EF的高

∴，解得或

∵P的匀速速度为每秒2个单位，AB=3，

∴P在AC上时，

∴．

故t的值为：2