题目内容
如图，正方形网格中的△ABC，若小方格边长为1，则△ABC的形状为（ ）分析：根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理进行判定，从而不难得到其形状．
解答：解：∵正方形小方格边长为1
∴BC=
=2
，
AC=
=
，
AB=
=
，
∵在△ABC中，BC2+AC2=52+13=65，AB2=65，
∴BC2+AC2=AB2，
∴△ABC是直角三角形．
故选A．
∴BC=
| 42+62 |
| 13 |
AC=
| 22+32 |
| 13 |
AB=
| 12+82 |
| 65 |
∵在△ABC中，BC2+AC2=52+13=65，AB2=65，
∴BC2+AC2=AB2，
∴△ABC是直角三角形．
故选A．
点评：考查了勾股定理的逆定理，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
相关题目
（1）先化简，再求值：x（x-2）-（x+1）（x-1），其中x=10．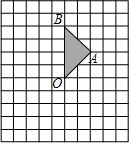
如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABO的三个顶点A，B，O都在格点上．