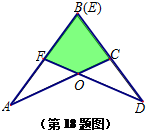
题目内容
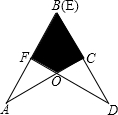 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分为△AOF、△DOC.
两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分为△AOF、△DOC.(1)求证:△AOF≌△DOC.
(2)连接BO,AD,试判断直线BO与线段AD的关系.(只写结论,不要求证明)
分析:(1)根据题意AB=BD,AC=DF,∠A=∠D,AB=BD,AC=DF可得AF=DC,利用AAS即可判定△AOF≌△DOC;
(2)首先根据已知得出FO=CO,即可得出△BFO≌△BCO,进而得出BG⊥AD.
(2)首先根据已知得出FO=CO,即可得出△BFO≌△BCO,进而得出BG⊥AD.
解答: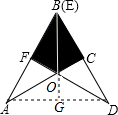 (1)证明:∵两块完全相同的三角形纸板ABC和DEF,
(1)证明:∵两块完全相同的三角形纸板ABC和DEF,
∴AB=BD,BF=BC,
∴AB-BF=BD-BC,
∴AF=DC
∵∠A=∠D,∠AOF=∠DOC,
在△AOF与△DOC中,
,
∴△AOF≌△DOC(AAS);
(2)直线BO与线段AD是垂直关系;
连接BO并延长到AD于点G,连接AD,
∵△AOF≌△DOC,
∴FO=CO,
在△BFO和△BCO中,
,
∴△BFO≌△BCO(SSS),
∴∠FBO=∠CBO,
∵AB=BD,
∴BG⊥AD.
 (1)证明:∵两块完全相同的三角形纸板ABC和DEF,
(1)证明:∵两块完全相同的三角形纸板ABC和DEF,∴AB=BD,BF=BC,
∴AB-BF=BD-BC,
∴AF=DC
∵∠A=∠D,∠AOF=∠DOC,
在△AOF与△DOC中,
|
∴△AOF≌△DOC(AAS);
(2)直线BO与线段AD是垂直关系;
连接BO并延长到AD于点G,连接AD,
∵△AOF≌△DOC,
∴FO=CO,
在△BFO和△BCO中,
|
∴△BFO≌△BCO(SSS),
∴∠FBO=∠CBO,
∵AB=BD,
∴BG⊥AD.
点评:此题主要考查了全等三角形判定与性质,解答此题的关键是根据题意得出AF=DC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
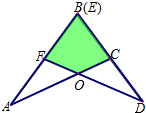 20、两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?
20、两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点,不重叠的两部分△AOF与△DOC是否全等?为什么?