题目内容
已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).
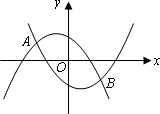
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当a=![]() 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线l,l1,l2都垂直于x轴,l1,l2分别经过A,B两点,l在直线l1,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值.
答案:
解析:
解析:
|
(1)解:答案不唯一,只要合理均可.例如: ①抛物线 ②抛物线 ③抛物线 ④抛物线 ⑤抛物线 ⑥抛物线 等等. 3分 (2)当 解得 ① ② ③ (3) 根据题意,得 说明:1.第(1)问每写对一条得1分; 2.第(2)问中,①②③任意写对一条得1分;其它结论参照给分. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
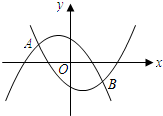 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值? 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;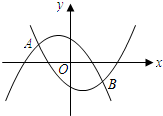 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值? 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
 (其中a为常数,且a>0)
(其中a为常数,且a>0)
 时,设
时,设 与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。
与x轴分别交于M、N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E、F两点(E在F的左边),观察M、N、E、F四点坐标,请写出一个你所得到的正确结论,并说明理由。  都垂直于x轴,
都垂直于x轴, 分别经过A、B两点,在直线
分别经过A、B两点,在直线 之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。
之间,且与两条抛物线分别交于C、D两点,求线段CD长的最大值。