题目内容
如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠DBE=∠DCE.其中正确结论的个数为( )
A.0 B.1 C.2 D.3

D.
详解:∵∠BAC=60°,∴∠ABC+∠ACB=180°-60 °=120°,
°=120°,
∵BE、CE分别为∠ABC、∠ACB的平分线,
∴∠EBC= ∠ABC,∠ECB=
∠ABC,∠ECB= ∠ACB,
∠ACB,
∴∠EBC+∠ECB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×120°=60°,
×120°=60°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°,故①正确;
如图,过点D作DF⊥AB于F,DG⊥AC 的
的 延长线于G,
延长线于G,

∵BE、CE分别为∠ABC、∠ACB的平分线,
∴AD为∠BAC的平分线,∴DF=DG,
∴∠FDG=360°-90°×2-60°=120°,
又∵∠BDC= 120°,
120°,
∴∠BDF+∠CDF=120°,∠CDG+∠CDF=120°,∴∠BDF=∠CDG,
∵在△BDF和△CDG中,∠BFD=∠CGD=9 0°,DF=DG,∠BDF=∠CDG,
0°,DF=DG,∠BDF=∠CDG,
∴△BDF≌ △CDG(ASA),∴DB=CD,∴∠DBC=
△CDG(ASA),∴DB=CD,∴∠DBC= (180°-120°)=30°,
(180°-120°)=30°,
∴∠DBE=∠DBC+∠CBE=30°+∠CBE,
∵BE平分∠ABC,AE平分∠BAC,∴∠ABE=∠CBE,∠BAE= ∠BAC=30°,
∠BAC=30°,
根据三角形的外角性质,∠DEB=∠ABE+∠BAE=∠ABE+30°,
∴∠DBE=∠DEB,∴DB=DE,故②正确;
∵DB=DE=DC,∴∠DBE=∠DCE,故③正确;
综上所述,正确的结论有①②③共3个.故选D.

 名校课堂系列答案
名校课堂系列答案为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办法,其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系:
| Ⅰ型收割机 | Ⅱ型收割机 | ||||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 补贴金额y(万元) | y1=kx | 2 | y2=ax2+bx | 2.4 | 3.2 |
(1)分别求出y1和y2的函数表达式;
(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的
方案,并求出按此方案能获得的补贴金额。

 的相反数是________;
的相反数是________;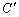 处,折痕为EF,若∠ABE=20°,那么∠
处,折痕为EF,若∠ABE=20°,那么∠ 的度数为____________.
的度数为____________.
 明理由.
明理由.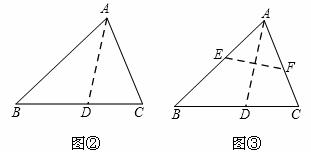

 B.
B. C.
C. D.
D. 
 -2x+10=0是关于x的一元二次方程,则m的值为( )
-2x+10=0是关于x的一元二次方程,则m的值为( ) D.±2
D.±2 ,则sinA的值为( )
,则sinA的值为( ) B.
B. C.
C.
 图的概率是( )
图的概率是( )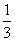 B.
B.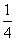 C.
C.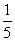 D.
D.