题目内容
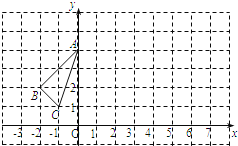
【题目】已知函数y=|x2﹣x﹣2|,直线y=kx+4恰好与y=|x2﹣x﹣2|的图象只有三个交点,则k的值为_____.
【答案】1﹣2![]() 或﹣2
或﹣2
【解析】
直线y=kx+4与抛物线y=-x2+x+2(-1≤x≤2)相切时,直线y=kx+4与y=|x2-x-2|的图象恰好有三个公共点,即-x2+x+2=kx+4有相等的实数解,利用根的判别式的意义可求出此时k的值,另外当y=kx+4过(2,0)时,也满足条件.
解:当y=0时,x2-x-2=0,解得x1=-1,x2=2,
则抛物线y=x2-x-2与x轴的交点为(-1,0),(2,0),
把抛物线y=x2-x-2图象x轴下方的部分沿x轴翻折到x轴上方,
则翻折部分的抛物线解析式为y=-x2+x+2(-1≤x≤2),
当直线y=kx+4与抛物线y=-x2+x+2(-1≤x≤2)相切时,
直线y=kx+4与函数y=|x2-x-2|的图象恰好有三个公共点,
即-x2+x+2=kx+4有相等的实数解,整理得x2+(k-1)x+2=0,△=(k-1)2-8=0,
解得k=1±2![]() ,
,
所以k的值为1+2![]() 或1-2
或1-2![]() .
.
当k=1+2![]() 时,经检验,切点横坐标为x=-
时,经检验,切点横坐标为x=-![]() <-1不符合题意,舍去.
<-1不符合题意,舍去.
当y=kx+4过(2,0)时,k=-2,也满足条件,
故答案为1-2![]() 或-2.
或-2.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目