题目内容
 (2013•鄂尔多斯)某校校园内有一个大正方形花坛,它由四个边长均为3米的小正方形组成,如图(1),且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图(2),DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
(2013•鄂尔多斯)某校校园内有一个大正方形花坛,它由四个边长均为3米的小正方形组成,如图(1),且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图(2),DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )分析:先求出△AEF和△DEG的面积,然后可得到五边形EFBCG的面积,继而可得y与x的函数关系式.
解答:解:S△AEF=
AE×AF=
x2,S△DEG=
DG×DE=
×1×(3-x)=
,
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-
x2-
=-
x2+
x+
,
则y=4×(-
x2+
x+
)=-2x2+2x+30.5,
∵AE<AD,
∴x<3,
综上可得:y=-2x2+2x+30.5(x<3).
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3-x |
| 2 |
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-
| 1 |
| 2 |
| 3-x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
则y=4×(-
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
∵AE<AD,
∴x<3,
综上可得:y=-2x2+2x+30.5(x<3).
故选A.
点评:本题考查了动点问题的函数图象,解答本题的关键是求出y与x的函数关系式,对于有些题目可以不用求出函数关系式,根据走势或者特殊点的值进行判断.

练习册系列答案
相关题目
 (2013•鄂尔多斯)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型(如图所示)摆出相同姿势,才能穿墙而过,否则会被推入水池.若墙上的三个空洞恰是某个几何体的三视图,则该几何体为( )
(2013•鄂尔多斯)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型(如图所示)摆出相同姿势,才能穿墙而过,否则会被推入水池.若墙上的三个空洞恰是某个几何体的三视图,则该几何体为( )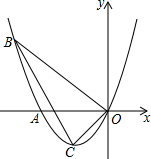 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.