题目内容
将1，2，3…100，这100个自然数任意分成50组，每组两个数，将其中一个数记为a，另一个数记为b，代入代数式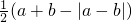
中计算，求出其结果，50组都代入后可得50个值，求这50个值的和的最小值（请简要说明理由）．
解：最小值为1275．
理由如下：假设a＞b，
则
（a+b-|a-b|）=（a+b-a+b）=b，
所以，当50组中的较小的数b恰好是1到50时，这50个值的和最小，
最小值为1+2+3+…+50=
=1275．
分析：不妨设各组中的数的a比b大，然后去掉绝对值号化简为b，所以当50组中的较小的数恰好是1到50时，这50个值的和最小，再根据求和公式列式计算即可得解．
点评：本题考查了代数式求值，通过假设，把所给代数式化简，然后判断出各组中的b值恰好是1到50这50个数时取得最小值时解题的关键．
理由如下：假设a＞b，
则
（a+b-|a-b|）=（a+b-a+b）=b，所以，当50组中的较小的数b恰好是1到50时，这50个值的和最小，
最小值为1+2+3+…+50=
=1275．分析：不妨设各组中的数的a比b大，然后去掉绝对值号化简为b，所以当50组中的较小的数恰好是1到50时，这50个值的和最小，再根据求和公式列式计算即可得解．
点评：本题考查了代数式求值，通过假设，把所给代数式化简，然后判断出各组中的b值恰好是1到50这50个数时取得最小值时解题的关键．
练习册系列答案
相关题目
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表：
现将两种食物混合成100千克的混合食品．设混合食品中甲、乙食物含量分别为x（千克）和y（千克），如果混合食品中要求维生素A不低于40000单位，B不低于28000单位．
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
（1）求x的取值范围；
（2）当甲、乙各取多少千克时，符合题意的混合食品成本最低？并求该最低成本价．
