题目内容
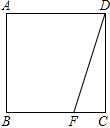 如图,正方形ABCD,点F在BC上,试在图中画出一条线段,构出另一个三角形,使得这个三角形全等于△DFC.
如图,正方形ABCD,点F在BC上,试在图中画出一条线段,构出另一个三角形,使得这个三角形全等于△DFC.(1)你能在图中画出几种不同位置的线段得到这个三角形?试写出能够画出的种数共有
8
8
种.(2)画出其中的1种位置的线段,并证明你构出的三角形全等于△DFC.
分析:(1)从正方形的每个顶点出发可以构出2个满足条件的三角形,扣除其中一个与△DFC重合,余7个三角形,又过点F作AD的垂线段可以构出1个满足条件的三角形,所以可以构出8个满足条件的三角形;
(2)利用“边角边”证明两三角形全等即可.
(2)利用“边角边”证明两三角形全等即可.
解答:解:(1)如图,共可以构造出8个满足条件的三角形;
故答案为:8.
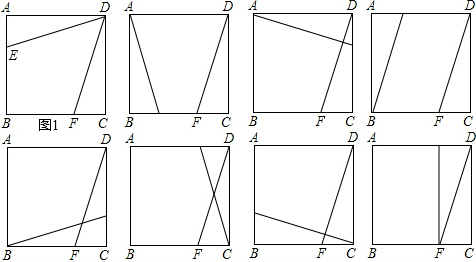
(2)如图1,作AE=CF,则△DFC≌△DAE,
证明如下:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠C=90°,
在△DFC和△DAE中,
,
∴△DFC≌△DAE(SAS).
故答案为:8.

(2)如图1,作AE=CF,则△DFC≌△DAE,
证明如下:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠C=90°,
在△DFC和△DAE中,
|
∴△DFC≌△DAE(SAS).
点评:本题考查了正方形的性质,全等三角形的判定,确定出每一个顶点可以作出两个满足条件的三角形是解题的关键,容易漏掉从点F作出的线段而导致出错.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.