题目内容
 (2012•密云县一模)已知:x1、x2分别为关于x的一元二次方程mx2+2x+2-m=0的两个实数根.
(2012•密云县一模)已知:x1、x2分别为关于x的一元二次方程mx2+2x+2-m=0的两个实数根.(1)设x1、x2均为两个不相等的非零整数根,求m的整数值;
(2)利用图象求关于m的方程x1+x2+m-1=0的解.
分析:(1)先根据球根公式用m表示出x1、x2的值,再根据x1、x2均为非0整数即可得出m的值;
(2)将x1、x2的值代入关于m的方程x1+x2+m-1=0,设y1=
,y2=m-1,并在同一直角坐标系中分别画出y1与y2的图象,根据两函数图象的交点坐标即可求出方程的解.
(2)将x1、x2的值代入关于m的方程x1+x2+m-1=0,设y1=
| 2 |
| m |
解答: 解:(1)∵△=22-4×m×(2-m)=4(1-m)2,
解:(1)∵△=22-4×m×(2-m)=4(1-m)2,
∴由求根公式,得x1=
=1-
,x2=-1.
要使x1,x2均为整数,
必为整数.
∴当m取±1、±2时,x1,x2均为整数.
又∵当m=1时,x1=x2=-1,
∴舍m=1.
当m=2时,x1=1-
=0,
∴m=2(舍去).
∴m的值为-1和-2;
(2)将x1=
,x2=-1代入方程 x1+x2+m-1=0,
整理得
=m-1.
设y1=
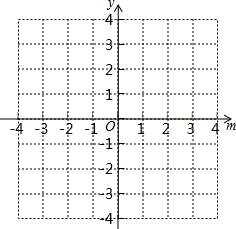
,y2=m-1,并在同一直角坐标系中分别画出y1与y2的图象(如图所示).
由图象可得,关于m的方程x1+x2+m-1=0的解为m1=-1,m2=2.
 解:(1)∵△=22-4×m×(2-m)=4(1-m)2,
解:(1)∵△=22-4×m×(2-m)=4(1-m)2,∴由求根公式,得x1=
| m-2 |
| m |
| 2 |
| m |
要使x1,x2均为整数,
| 2 |
| m |
∴当m取±1、±2时,x1,x2均为整数.
又∵当m=1时,x1=x2=-1,
∴舍m=1.
当m=2时,x1=1-
| 2 |
| m |
∴m=2(舍去).
∴m的值为-1和-2;
(2)将x1=
| m-2 |
| m |
整理得
| 2 |
| m |
设y1=
| 2 |
| m |
由图象可得,关于m的方程x1+x2+m-1=0的解为m1=-1,m2=2.
点评:本题考查的是根的判别式及反比例函数的应用,能利用数形结合求出方程的解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
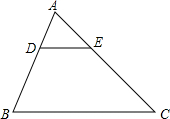 (2012•密云县一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为( )
(2012•密云县一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为( )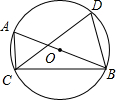 (2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是
(2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是