题目内容
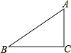
【题目】如图,在![]() 中.
中.![]() ,
,![]() ,
,![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
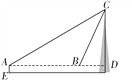
本题中直角三角形的角不是特殊角,故过A作AD交BC于D,使∠BAD=15°,根据三角形内角和定理可求出∠DAC及∠ADC的度数,再由特殊角的三角函数值及勾股定理求解即可.
过A作AD交BC于D,使∠BAD=15°,
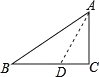
∵△ABC中,∠ACB=90°,∠ABC=15°,
∴∠BAC=75°,
∴∠DAC=∠BAC∠BAD=75°15°=60°,
∴∠ADC=90°∠DAC=90°60°=30°,
∴AC=![]() AD,
AD,
又∵∠ABC=∠BAD=15°
∴BD=AD,
∵BC=1,
∴AD+DC=1,
CD=x,则AD=1x,AC=![]() (1x),
(1x),
∴AD2=AC2+CD2,即(1x)2=![]() (1x)2+x2,
(1x)2+x2,
解得:x=3+2![]() ,
,
∴AC=![]() (42
(42![]() )=2
)=2![]() ,
,
故选:B.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如右表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.