��Ŀ����
����Ŀ����֪����y=  ��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
������M1��x1 �� y1����M2��x2 �� y2����ͼ���ϣ���x1��x2��0����y1��y2��
�ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ�
�����۵�P��ʲôλ�ã�ʼ����S��AOB=7.5��AP=4BP��
�ܵ���P�ƶ���ʹ��AOB=90��ʱ����A������Ϊ��2 ![]() ����
���� ![]() ����
����
������ȷ�Ľ��۸���Ϊ�� ��
A.1
B.2
C.3
D.4
���𰸡�C
���������⣺�ٴ���x1��x2��0������y��x���������С����y1��y2 �� �ʢٴ���
����ȷ����P��0����3����
��B����1����3����A��4����3����
��AB=5��OA= ![]() =5��
=5��
��AB=AO��
���AOB�ǵ��������Σ��ʢ���ȷ��
����ȷ����P��0��m������B�� ![]() ��m����A����
��m����A���� ![]() ��m����
��m����
��PB=�� ![]() ��PA=��
��PA=�� ![]() ��
��
��PA=4PB��
��SAOB=S��OPB+S��OPA= ![]() +
+ ![]() =7.5���ʢ���ȷ��
=7.5���ʢ���ȷ��
����ȷ����P��0��m������B�� ![]() ��m����A����
��m����A���� ![]() ��m����
��m����
��PB=�� ![]() ��PA=��
��PA=�� ![]() ��OP=��m��
��OP=��m��
�ߡ�AOB=90�㣬��OPB=��OPA=90�㣬
���BOP+��AOP=90�㣬��AOP+��OPA=90�㣬
���BOP=��OAP��
���OPB�ס�APO��
�� ![]() =
= ![]() ��
��
��OP2=PBPA��
��m2=�� ![]() ����
���� ![]() ����
����
��m4=36��
��m��0��
��m=�� ![]() ��
��
��A��2 ![]() ����
���� ![]() �����ʢ���ȷ��
�����ʢ���ȷ��
��ڢۢ���ȷ��
��ѡC��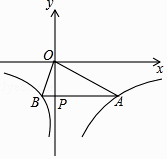
�����㾫����������Ŀ����֪����������һ�κ��������ʺ͵��������ε��ж������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С�����һ������������������ȣ���ô�����������Եı�Ҳ��ȣ���ƣ��ȽǶԵȱߣ�������ж�����������֤��ͬһ���������еı���ȣ�