题目内容
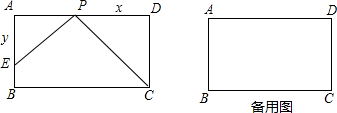
如图所示，已知矩形ABCD，沿对角线AC把△DAC翻折，AD′与BC相交于点E，判断△AEC的形状．
解：△AEC为等腰三角形．
理由：由折叠的性质可知∠DAC=∠D′AC，
∵AD∥BC，
∴∠DAC=∠ACB，
∴∠D′AC=∠ACB，
∴△AEC为等腰三角形．
分析：由折叠的性质可知∠DAC=∠D′AC，由AD∥BC可知∠DAC=∠ACB，可证△AEC为等腰三角形．
点评：本题考查了折叠的性质，平行线的性质，等腰三角形的判定．关键是利用角相等过渡到同一个三角形中．
理由：由折叠的性质可知∠DAC=∠D′AC，
∵AD∥BC，
∴∠DAC=∠ACB，
∴∠D′AC=∠ACB，
∴△AEC为等腰三角形．
分析：由折叠的性质可知∠DAC=∠D′AC，由AD∥BC可知∠DAC=∠ACB，可证△AEC为等腰三角形．
点评：本题考查了折叠的性质，平行线的性质，等腰三角形的判定．关键是利用角相等过渡到同一个三角形中．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
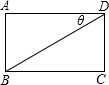如图所示，已知矩形ABCD（AD＞AB）中，AB=a，∠BDA=θ，试用a与θ表示：AD=
如图所示，已知矩形ABCD的边AB=3cm，AD=4cm．
如图所示，已知矩形ABCD中两条对角线AC、BD相交于点O，∠ADB=30°，DF∥AC交BC的延长线于F点，