Question

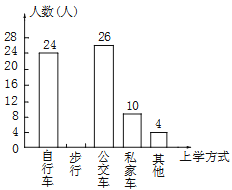
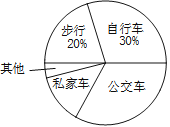
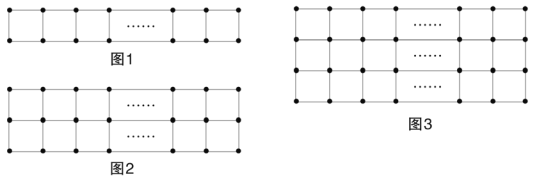
【题目】现有a枚棋子，按图1的方式摆放时刚好围成m个小正方形，按图2的方式摆放刚好围成2n个小正方形。

（1）用含m的代数式表示a，有a＝ ；用含n的代数式表示a，有a＝ ；

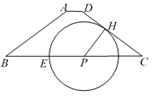
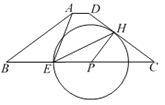
（2）若这a枚棋子按图3的方式摆放恰好围成3p个小正方形，

①P的值能取7吗？请说明理由；

②直接写出a的最小值：

Answer 1

【答案】（1）2m+2，3n+3；（2）①能，理由见解析；②8

【解析】

（1）根据图1每多一个正方形多用2枚棋子，写出摆放m个正方形所用的棋子的枚数；根据图2在两个小正方形的基础上，每多2个正方形多用3枚棋子，写出摆放2n个小正方形所用的棋子的枚数；

（2）①根据图3在三个小正方形的基础上，每多3个正方形多用4枚棋子，写出摆放3p个小正方形所用的棋子的枚数，当P的值取7时，可得出21个正方形共用32枚棋子；所以p可以取7；

②根据图3的摆放方式可得最少摆放三个正方形，可得出a的最小值

解：（1）由图可知，图1每多1个正方形，多用2枚棋子，

∴m个小正方形共用4+2(m-1)=2m+2枚棋子；
由图可知，图2两个小正方形的基础上，每多2个正方形多用3枚棋子，

∴2n个小正方形共用6+3(n-1)=3n+3 枚棋子；
故答案为：2m+2，3n+3；

（2）p可以取7

①根据图3在三个小正方形的基础上，每多3个正方形多用4枚棋子，

∴3p个小正方形共用8+4(p-1)=4p+4 枚棋子；

当p=7时，即21个正方形共用32枚棋子；

②根据图3的摆放方式可得最少摆放三个正方形，

∴a的最小值为：8

故答案为：8