题目内容
 (2013•大连一模)如图,直线l1:y=4x与直线l2:y=-
(2013•大连一模)如图,直线l1:y=4x与直线l2:y=-| 4 |
| 3 |
| 20 |
| 3 |
(1)求点A的坐标;
(2)求S与t的函数关系式,并写出t的取值范围;
(3)在点P的运动过程中,DP能否为4
| 2 |
分析:(1)由直线l1:y=4x与直线l2:y=-
x+
相交于点A,联立可得方程组:
,解此方程组即可求得点A的坐标;
(2)由OC⊥l2,即可求得直线OC的解析式,由OP=t,即可求得点P的坐标,由两点式,即可求得DP2的值,联立直线OC与直线l2:y=-
x+
,即可求得点C的坐标,即可求得OC的长,即可得t的取值范围;
(3)由DP=4
与(2)中S与t的函数关系式,可得方程S=t2-6t+25=32,解此方程,又由0≤t≤4,即可判定点P的运动过程中DP不能为4
.
| 4 |
| 3 |
| 20 |
| 3 |
|
(2)由OC⊥l2,即可求得直线OC的解析式,由OP=t,即可求得点P的坐标,由两点式,即可求得DP2的值,联立直线OC与直线l2:y=-
| 4 |
| 3 |
| 20 |
| 3 |
(3)由DP=4
| 2 |
| 2 |
解答:解:(1)∵直线l1:y=4x与直线l2:y=-
x+
相交于点A,
∴可得方程组:
,
解得:
,
∴点A的坐标为(
,5);
(2)∵点A的坐标为(
,5),
∴D(0,5),
∵OC⊥l2,直线l2的斜率为-
,
∴直线OC的斜率为
,
∴直线OC的解析式为:y=
x,
联立直线OC与直线l2:y=-
x+
,可得方程组:
,
解得:
,
∴点C的坐标为(
,
),
∴OC=
=4,
∵OP=t(0≤OP≤OC),
过点P作PE⊥OB于E,
∵tan∠POE=
,
∴cos∠POE=
,sin∠POE=
,
∴P点的坐标为(
t,
t),
∴DP2=(
t-0)2+(
t-5)2=t2-6t+25,
∴S与t的函数关系为S=t2-6t+25(0≤t≤4);
(3)不能;
理由:若DP=4
,
则S=DP2=(4
)2=32,
即S=t2-6t+25=32,
解得:t=7或t=-1(舍去),
∵0≤t≤4,
∴t=7不符合题意,
∴点P的运动过程中DP不能为4
.
| 4 |
| 3 |
| 20 |
| 3 |
∴可得方程组:
|
解得:
|
∴点A的坐标为(
| 5 |
| 4 |
(2)∵点A的坐标为(
| 5 |
| 4 |
∴D(0,5),
∵OC⊥l2,直线l2的斜率为-
| 4 |
| 3 |
∴直线OC的斜率为
| 3 |
| 4 |
∴直线OC的解析式为:y=
| 3 |
| 4 |
联立直线OC与直线l2:y=-
| 4 |
| 3 |
| 20 |
| 3 |
|
解得:
|
∴点C的坐标为(
| 16 |
| 5 |
| 12 |
| 5 |

∴OC=
(
|
∵OP=t(0≤OP≤OC),
过点P作PE⊥OB于E,
∵tan∠POE=
| 3 |
| 4 |
∴cos∠POE=
| 4 |
| 5 |
| 3 |
| 5 |
∴P点的坐标为(
| 4 |
| 5 |
| 3 |
| 5 |
∴DP2=(
| 4 |
| 5 |
| 3 |
| 5 |
∴S与t的函数关系为S=t2-6t+25(0≤t≤4);
(3)不能;
理由:若DP=4
| 2 |
则S=DP2=(4
| 2 |
即S=t2-6t+25=32,
解得:t=7或t=-1(舍去),
∵0≤t≤4,
∴t=7不符合题意,
∴点P的运动过程中DP不能为4
| 2 |
点评:此题属于一次函数的综合题,考查了待定系数求一次函数解析式,两点式、函数交点问题以及方程组的解法.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
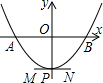 (2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
(2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( ) (2013•大连一模)如图是由四个完全相同的正方体组成的几何体,这个几何体的俯视图是( )
(2013•大连一模)如图是由四个完全相同的正方体组成的几何体,这个几何体的俯视图是( )