题目内容
如图,已知点A(8,0),sin∠ABO=
,抛物线经过点O、A,且顶点在△AOB的外接圆上,则此抛物线的解析式为( )

| 4 |
| 5 |
A.y=-
| B.y=-
| ||||||||
C.y=
| D.y=-
|

如图所示:连接AC,过圆心O′作EF⊥OA,
∵∠AOC=90°,∠ABO=∠OCA,
∴
=
,
∵点A(8,0),
∴AC=10,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴MF=2,
∴F点坐标为:(4,-2),
设过O,A,F的抛物线解析式为:y=a(x-4)2-2,
将A代入(8,0)得:
0=a(8-4)2-2,
解得:a=
,
∴此时抛物线解析式为:y=
(x-4)2-2=
x2-x,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴ME=8,
∴E点坐标为:(4,8),
设过O,A,E的抛物线解析式为:y=a(x-4)2+8,
将A代入(8,0)得:
0=a(8-4)2+8,
解得:a=-
,
∴此时抛物线解析式为:y=-
(x-4)2+8=-
x2+x,
故选:D.

∵∠AOC=90°,∠ABO=∠OCA,
∴
| AO |
| AC |
| 4 |
| 5 |
∵点A(8,0),
∴AC=10,
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴MF=2,
∴F点坐标为:(4,-2),
设过O,A,F的抛物线解析式为:y=a(x-4)2-2,
将A代入(8,0)得:
0=a(8-4)2-2,
解得:a=
| 1 |
| 8 |
∴此时抛物线解析式为:y=
| 1 |
| 8 |
| 1 |
| 8 |
根据题意得出:AM=OM=4,AO′=5,
∴MO′=3,∴ME=8,
∴E点坐标为:(4,8),
设过O,A,E的抛物线解析式为:y=a(x-4)2+8,
将A代入(8,0)得:
0=a(8-4)2+8,
解得:a=-
| 1 |
| 2 |
∴此时抛物线解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
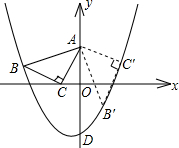 中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).

 ),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
),B(4,0),△AOB绕O点按逆时针方向旋转90°得到△COD.
