题目内容
如图，在⊙O中，AB为⊙O的直径，AC是弦，OC=4，∠OAC=60°．动点M从A点出发，以每秒π个单位的速度在⊙O上按逆时针方向运动一周．设动点M的运动时间为t（s）．当t为何值时，以点A、M、B、C为顶点的四边形是轴对称图形．
解：如图1，当点M运动到与点C关于AB轴对称即点M1处时，四边形AMBC是轴对称图形
∴弧AM1的长度为：
，∴t1=
如图2，当点M运动到点M2处时，四边形AMBC是矩形
∴弧AM2的长度为：
∴t2=
如图3，当点M运动到点M3处时，四边形ABMC是等腰梯形
∴弧ABM3的长度为：
，∴t3=
∴当t=、或时，以点A、M、B、C为顶点的四边形是轴对称图形．
分析：做题首先考虑我们课本中的轴对称图形，然后分类讨论计算出时间t．
点评：本题主要考查弧长的计算，涉及的知识点很多，有轴对称图形，等腰三角形的性质，综合性比较强．
∴弧AM1的长度为：
，∴t1=如图2，当点M运动到点M2处时，四边形AMBC是矩形
∴弧AM2的长度为：
∴t2=如图3，当点M运动到点M3处时，四边形ABMC是等腰梯形
∴弧ABM3的长度为：
，∴t3=∴当t=
、或时，以点A、M、B、C为顶点的四边形是轴对称图形．分析：做题首先考虑我们课本中的轴对称图形，然后分类讨论计算出时间t．
点评：本题主要考查弧长的计算，涉及的知识点很多，有轴对称图形，等腰三角形的性质，综合性比较强．
练习册系列答案
相关题目
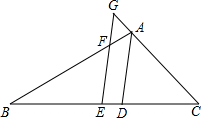如图，在△ABC中，AB＞AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．
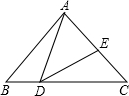如图，在△ABC中，AB=AC，D为BC边上一点，且∠BAD=30°，若AD=DE，∠EDC=33°，则∠DAE的度数为
如图，在△ABC中，AB=AC，D是△ABC内一点，且BD=DC．求证：∠ABD=∠ACD．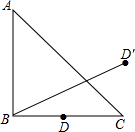
如图，在△ABC中，AB=BC，∠ABC=90°，D是BC的中点，且它关于AC的对称点是D′，BD′=
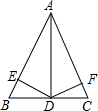如图，在△ABC中，AB=AC，D点是BC的中点，DE⊥AB于E点，DF⊥AC于F点，则图中全等三角形共有