题目内容
已知：x1，x2是一元二次方程x2+2ax+b=0的两根，且x1+x2=3，x1x2=1，则a、b的值分别是
- A.a=-3，b=1
- B.a=3，b=1
- C.
，b=-1 - D.，b=1
D
分析：先根据根与系数的关系可得x1+x2=-2a，x1x2=b，而x1+x2=3，x1x2=1，那么-2a=3，b=1，解即可．
解答：∵x1，x2是一元二次方程x2+2ax+b=0的两根，
∴x1+x2=-2a，x1x2=b，
∵x1+x2=3，x1x2=1，
∴-2a=3，b=1，
即a=-
，b=1，
故选D．
点评：本题考查了根与系数的关系，解题的关键是掌握根与系数的等量关系的公式．
分析：先根据根与系数的关系可得x1+x2=-2a，x1x2=b，而x1+x2=3，x1x2=1，那么-2a=3，b=1，解即可．
解答：∵x1，x2是一元二次方程x2+2ax+b=0的两根，
∴x1+x2=-2a，x1x2=b，
∵x1+x2=3，x1x2=1，
∴-2a=3，b=1，
即a=-
，b=1，故选D．
点评：本题考查了根与系数的关系，解题的关键是掌握根与系数的等量关系的公式．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知数据x1，x2，…，xn的平均数是4，则一组新数据x1+7，x2+7，…，xn+7的平均数是（ ）
| A、4 | B、3 | C、11 | D、7 |
，
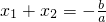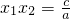．这一结论称为一元二次方程根与系数关系，它的应用很多，请完成下列各题：