题目内容
 四边形ABCD中,AC和BD交于点E,若AC平分∠DAB,且AB=AE,AC=AD,有以下四个命题:①AC⊥BD;②BC=DE;③∠DBC=
四边形ABCD中,AC和BD交于点E,若AC平分∠DAB,且AB=AE,AC=AD,有以下四个命题:①AC⊥BD;②BC=DE;③∠DBC= ∠DAB;④AB=BE=AE.其中命题一定成立的是
∠DAB;④AB=BE=AE.其中命题一定成立的是
- A.①②
- B.②③
- C.①③
- D.②④
B
分析:根据等腰三角形的性质,等边三角形的判定,圆内接四边形的性质,全等三角形的性质判断各选项是否正确即可.
解答:∵AB=AE,一个三角形的直角边和斜边一定不相等,∴AC不垂直于BD,①错误;
利用边角边定理可证得△ADE≌△ABC,那么BC=DE,②正确;
由△ADE≌△ABC可得∠ADE=∠ACB,那么A,B,C,D四点共圆,∴∠DBC=∠DAC= ∠DAB,③正确;
∠DAB,③正确;
△ABE不一定是等边三角形,那么④不一定正确;
②③正确,故选B.
点评:此题主要考查了全等三角形的性质,以及直角三角形中斜边最长;全等三角形的对应边相等;等边三角形的三边相等.
分析:根据等腰三角形的性质,等边三角形的判定,圆内接四边形的性质,全等三角形的性质判断各选项是否正确即可.
解答:∵AB=AE,一个三角形的直角边和斜边一定不相等,∴AC不垂直于BD,①错误;
利用边角边定理可证得△ADE≌△ABC,那么BC=DE,②正确;
由△ADE≌△ABC可得∠ADE=∠ACB,那么A,B,C,D四点共圆,∴∠DBC=∠DAC=
 ∠DAB,③正确;
∠DAB,③正确;△ABE不一定是等边三角形,那么④不一定正确;
②③正确,故选B.
点评:此题主要考查了全等三角形的性质,以及直角三角形中斜边最长;全等三角形的对应边相等;等边三角形的三边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.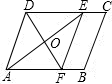 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.