Question

【题目】如图，△ABC中，点O是∠BCA与∠ABC的平分线的交点，过O作与BC平行的直线分别交AB、AC于D、E．已知△ABC的周长为15，BC的长为6，求△ADE的周长．

Answer 1

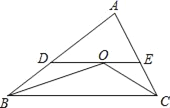
【答案】△ADE的周长为9．

【解析】

先利用角平分线的定义和平行线的性质得到∠1＝∠2，所以DB＝DO，同理可得EO＝CE，利用等线段代换得到△ADE的周长＝AB+AC，然后利用△ABC的周长为15得到AB+AC＝9，从而得到△ADE的周长．

∵点O是∠BCA与∠ABC的平分线的交点，∴∠1＝∠3．

∵DE∥BC，∴∠2＝∠3，∴∠1＝∠2，∴DB＝DO，同理可得：EO＝CE，∴△ADE的周长＝AD+AE+DE＝AD+DO+AE+OE＝AD+BD+AE+CE＝AB+AC．

∵△ABC的周长为15，∴AB+AC+BC＝15，而BC的长为6，∴AB+AC＝9，∴△ADE的周长为9．