题目内容
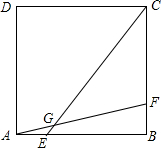 附加题:已知正方形ABCD的面积35平方厘米,E、F分别为边AB、BC上的点,AF和CE相交于点G,并且△ABF的面积为5平方厘米,△BCE的面积为14平方厘米,求四边形BEGF的面积.
附加题:已知正方形ABCD的面积35平方厘米,E、F分别为边AB、BC上的点,AF和CE相交于点G,并且△ABF的面积为5平方厘米,△BCE的面积为14平方厘米,求四边形BEGF的面积.
分析:要求四边形EGFB的面积,可将这个四边形分割成两个与三角形AEG,GFC等高的三角形,然后通过求它们底边的比来求面积.连接BG,那么三角形EGB和三角形AEG等高,三角形FBG和CFG等高,然后再求他们的底边比,如果连接AC,那么可根据三角形ABC的面积和ECB的面积,求出BE,AB的比例关系,也就求出了AE,BE的比例关系,同理可得出CF,BF的比例关系.也就求出了三角形AEG,EGB的面积比以及三角形CFG,BFG的面积比.然后根据三角形AGE+四边形EGFB(即两个小三角形的面积和)=三角形ABG的面积,三角形CFG的面积+四边形GFBE的面积=三角形CEB的面积,可列出关于组成四边形GFBE的两个小三角形面积的方程组,即可求出这两个小三角形的面积,进而可求出四边形的面积.
解答: 解:∵
解:∵
=
=
,同理
=
,如图,连BG.
记S△AGE=a,S△EGB=b,S△BGF=c,S△FGC=d.
则有a=
b,d=
c
由已知a+b+c=5,b+c+d=14,
即:
可求得:b=
,c=
.
因此:SBEGF=b+c=
=4
(平方厘米)
 解:∵
解:∵| BF |
| BC |
| S△ABF |
| S△ABC |
| 2 |
| 7 |
| BE |
| BA |
| 4 |
| 5 |
记S△AGE=a,S△EGB=b,S△BGF=c,S△FGC=d.
则有a=
| 1 |
| 4 |
| 5 |
| 2 |
由已知a+b+c=5,b+c+d=14,
即:
|
可求得:b=
| 28 |
| 27 |
| 100 |
| 27 |
因此:SBEGF=b+c=
| 128 |
| 27 |
| 20 |
| 27 |
点评:本题主要考查了正方形的性质和三角形面积的求法.本题主要应用的是两三角形等高(或等底)的情况下,底(或高)的比就等于面积比.

练习册系列答案
相关题目