题目内容

一个直角三角形三条边的长度是3，4，5．如果分别以各边为轴旋转一周，得到三个立体，那么三个立体中最大的体积和最小的体积的比是________．

5：3
分析：分别求出以3，4，5为轴旋转一周，得到三个立体的体积，比较出最大体积和最小体积，然后求出比值即可．
解答：以3为轴旋转一周，得到的立体的体积= $\text{[math]}$ πr²•3=16π，
以4为轴旋转一周，得到的立体的体积= $\text{[math]}$ πr²•4=12π，
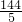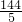以5为轴旋转一周，得到的立体的体积= $\text{[math]}$ π（ $\text{[math]}$ ）²• $\text{[math]}$ + $\text{[math]}$ π•（ $\text{[math]}$ ）²• $\text{[math]}$ = $\text{[math]}$ × $\text{[math]}$ π=9.6π，
∴三个立体中最大的体积和最小的体积的比=16π：9.6π=5：3．
故答案为：5：3．
点评：本题考查了勾股定理，圆的面积公式，圆的体积公式求解．
注意：绕直角三角形的斜边旋转一周得出的图形应该是两个圆锥的组合体．

练习册系列答案

状元坊广东中考备考用书系列答案

百年学典中考风向标系列答案

百校联盟中考冲刺名校模拟卷系列答案

夺A闯关一路领先中考模拟密卷系列答案

中考先锋滚动迁移复习法系列答案

琢玉计划寒假生活系列答案

决胜中考系列答案

书屯文化期末寒假期末冲刺假期作业云南人民出版社系列答案

硕源教育中考总复习名师解密系列答案

初中学业水平测试用书激活中考系列答案

相关题目

阅读材料并解答问题：
我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．
关于勾股定理的研究还有一个很重要的内容是勾股数组，在《几何》课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
方法1：若m为奇数（m≥3），则a=m，b=

（m²-1）和c=

（m²+1）是勾股数．
方法2：若任取两个正整数m和n（m＞n），则a=m²-n²，b=2mn，c=m²+n²是勾股数．
（1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
（2）请根据方法1和方法2按规律填写下列表格：

（3）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树

一个三角形三条边的长分别为8、6、10，那么这个三角形是

三角形．（填“钝角”、“锐角”或“直角”）

相传2500年前，古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了直角三角形三边的关系：“任意直角三角形，都有两直角边的平方和等于斜边的平方．”这就是著名的“勾股

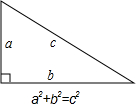定理”．它揭示了一个直角三角形三条边之间的数量关系（如图）．
根据“勾股定理”，我们就可以由已知两条直角边的长来求斜边的长．
如：a=1，b=1时，1²+1²=c²，c=

；a=1，b=2时，c=

；
…
请你根据上述材料，完成下列问题：
（1）a=1，b=3时，c=

；
（2）如果斜边长为

，则直角边为正整数

（3）请你在数轴上画出表示

的点（保留作图痕迹）．

我国是最早了解和应用勾股定理的国家之一，古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用，古希腊数学家毕达哥拉斯首先证明了勾股定理，在西方，勾股定理又称为“毕达哥拉斯定理”．
关于勾股定理的研究还有一个很重要的内容是勾股数组，在《几何》课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：
方法1：若m为奇数（m≥3），则a=m，b= $数学公式$ （m²-1）和c= $数学公式$ （m²+1）是勾股数．
方法2：若任取两个正整数m和n（m＞n），则a=m²-n²，b=2mn，c=m²+n²是勾股数．
（1）在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
（2）请根据方法1和方法2按规律填写下列表格：

（3）某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树______棵．