题目内容
如图，四边形ABCD内接于以BC为直径的圆，圆心为O，且AB=AD，延长CB、DA交于P，过C点作PD的垂线交PD的延长线于E，且PB=BO，连接OA．（1）求证：OA∥CD；
（2）求线段BC：DC的值；
（3）若CD=18，求DE的长．
分析：（1）连接BD，由圆周角定理可知∠BDC=90°，即CD⊥BD，再由AB=AD可知
=
，则OA⊥BD，由此即可得出结论；
（2）设⊙O的半径为r，则PB=OB=OC=OA=r，再由OA∥CD可知，△OAP∽△CDP，故可得出
=
，故可用r表示出CD的长，再求出BC：DC的值即可；
（3）由OF∥CD，OB=OC根据中位线定理可以求出OF，AF；再根据勾股定理在Rt△DBC中可以求出BD，DF；接着在Rt△ADF中求出AD；然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC，利用相似三角形的对应边成比例可以求出DE．
 |
| AB |
|
| AD |
（2）设⊙O的半径为r，则PB=OB=OC=OA=r，再由OA∥CD可知，△OAP∽△CDP，故可得出
| OP |
| PC |
| OA |
| CD |
（3）由OF∥CD，OB=OC根据中位线定理可以求出OF，AF；再根据勾股定理在Rt△DBC中可以求出BD，DF；接着在Rt△ADF中求出AD；然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC，利用相似三角形的对应边成比例可以求出DE．
解答：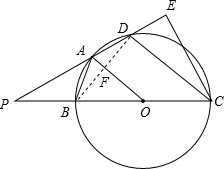
（1）证明：连接BD，交OA于点F．
∵BC是⊙O的直径，
∴∠BDC=90°，即CD⊥BD，
∵AB=AD，
∴
=
∴OA⊥BD，
∴OA∥CD；
（2）解：设⊙O的半径为r，
∵PB=OB，
∴PB=OB=OC=OA=r，
∵OA∥CD，
∴△OAP∽△CDP，
∴
=
，
=
，解得CD=
，
∴
=
=
；
（3）解：∵OF∥CD，
=
=
，
∴OF=9，AF=3；
∵BD=
=6
，
∴DF=
BD=3
，
∴AD=
=6
；
∵∠AFD=∠DEC=90°，OA∥DC，∠FAD=∠CDE，
∴△AFD∽△DEC，
∴
=
，即
=
；
∴DE=
．
（1）证明：连接BD，交OA于点F．∵BC是⊙O的直径，
∴∠BDC=90°，即CD⊥BD，
∵AB=AD，
∴
|
| AB |
|
| AD |
∴OA⊥BD，
∴OA∥CD；
（2）解：设⊙O的半径为r，
∵PB=OB，
∴PB=OB=OC=OA=r，
∵OA∥CD，
∴△OAP∽△CDP，
∴
| OP |
| PC |
| OA |
| CD |
| 2r |
| 3r |
| r |
| CD |
| 3r |
| 2 |
∴
| BC |
| CD |
| 2r | ||
|
| 4 |
| 3 |
（3）解：∵OF∥CD，
| OF |
| DC |
| BO |
| BC |
| 1 |
| 2 |
∴OF=9，AF=3；
∵BD=
| BC2-DC2 |
| 7 |
∴DF=
| 1 |
| 2 |
| 7 |
∴AD=
| DF2+AF2 |
| 2 |
∵∠AFD=∠DEC=90°，OA∥DC，∠FAD=∠CDE，
∴△AFD∽△DEC，
∴
| DE |
| DC |
| AF |
| AD |
| DE |
| 18 |
| 3 | ||
6
|
∴DE=
9
| ||
| 2 |
点评：本题考查的是相似三角形的判定与性质，综合性比较强，此题把垂径定理，平行线分线段成比例，相似三角形的性质与判定，勾股定理，中位线定理等知识都放在圆的背景中，充分发挥这些知识的作用解题．
练习册系列答案
相关题目
如图，四边形ABCD的对角线AC与BD互相垂直平分于点O，设AC=2a，BD=2b，请推导这个四边形的性质．（至少3条）
如图，四边形ABCD的对角线AC、BD交于点P，过点P作直线交AD于点E，交BC于点F．若PE=PF，且AP+AE=CP+CF．
如图，四边形ABCD，AB=AD=2，BC=3，CD=1，∠A=90°，求∠ADC的度数．
如图，四边形ABCD为正方形，E是BC的延长线上的一点，且AC=CE，求∠DAE的度数．