��Ŀ����
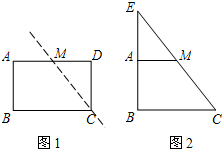 ��������״��ͼ1��ʾ�ľ���ֽƬABCD����ֱ��CM���������֣�����MΪAD���е㣮����������ֽƬ����ƴ��һЩ��ͼ�Σ�����ͼ2�е�Rt��BCE����ƴ�ɵ�һ��ͼ�Σ���������������ֽƬƴ�ɵ�Rt��BCE�ǵ���ֱ�������Σ���ԭ����ֽƬ�еı�AB��BC�ij��ֱ�Ϊa���ס�b���ף���a��bǡ���ǹ���x�ķ���x2-��m-1��x+m+1=0������ʵ�����������ԭ����ֽƬ�������
��������״��ͼ1��ʾ�ľ���ֽƬABCD����ֱ��CM���������֣�����MΪAD���е㣮����������ֽƬ����ƴ��һЩ��ͼ�Σ�����ͼ2�е�Rt��BCE����ƴ�ɵ�һ��ͼ�Σ���������������ֽƬƴ�ɵ�Rt��BCE�ǵ���ֱ�������Σ���ԭ����ֽƬ�еı�AB��BC�ij��ֱ�Ϊa���ס�b���ף���a��bǡ���ǹ���x�ķ���x2-��m-1��x+m+1=0������ʵ�����������ԭ����ֽƬ����������������ݵ���ֱ�������οɵõ�a��b�Ĺ�ϵ�����ݸ���ϵ���Ĺ�ϵ�õ�����һ����ĸ��m�Ĺ�ϵ���������ԭ����ֽƬ�������
����⣺�����֪AB=CD=AE����BC=BE=AB+AE��
��BC=2AB����b=2a��
������֪a��2a�Ƿ���x2-��m-1��x+m+1=0��������
��a+2a=m-1��a•2a=m+1��
��2m2-13m-7=0�����m=7��m=-
��
�����飺���ڵ�m=-
��a+2a=-
a��0��
��m=-
���������⣬��ȥ��m=7�������⣬
��S����=ab=m+1=8��
��ԭ����ֽƬ�����Ϊ8cm2��
��BC=2AB����b=2a��
������֪a��2a�Ƿ���x2-��m-1��x+m+1=0��������
��a+2a=m-1��a•2a=m+1��
��2m2-13m-7=0�����m=7��m=-
| 1 |
| 2 |
�����飺���ڵ�m=-
| 1 |
| 2 |
| 3 |
| 2 |
��m=-
| 1 |
| 2 |
��S����=ab=m+1=8��
��ԭ����ֽƬ�����Ϊ8cm2��
���������⿼���˾��ε������Լ�����ֱ�������ε����ʣ�����������ҵ���ȵıߣ������غϣ�ƴ�ϣ����ߵõ���Ӧ�Ĺ�ϵ�����ø���ϵ����ϵ��⣮

��ϰ��ϵ�д�
 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
�����Ŀ



