题目内容
在直角梯形ABCD中，AD∥BC，AB⊥BC，E是CD的中点，且AB=AD+BC，△ABE是（ ）
| A、等腰三角形 | B、等腰直角三角形 | C、直角三角形 | D、等边三角形 |
分析：过E点作EF∥AD，根据已知得到EF是梯形ABCD的中位线，根据中位线的性质从而推出△ABE是等腰直角三角形．
解答：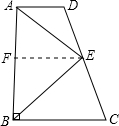
解：过E点作EF∥AD，
∵AD⊥AB
∴EF⊥AB
∵E为CD的中点
∴EF是梯形ABCD的中位线
∴2EF=AD+BC，EF是线段AB的垂直平分线，
∵AF=BF，AB=AD+BC，即EF=
AB，AE=BE，
∴∠AEB是直角
即△ABE是等腰直角三角形．
故选B．
解：过E点作EF∥AD，∵AD⊥AB
∴EF⊥AB
∵E为CD的中点
∴EF是梯形ABCD的中位线
∴2EF=AD+BC，EF是线段AB的垂直平分线，
∵AF=BF，AB=AD+BC，即EF=
| 1 |
| 2 |
∴∠AEB是直角
即△ABE是等腰直角三角形．
故选B．
点评：本题考查的是梯形中位线的性质及线段垂直平分线的性质．
练习册系列答案
相关题目
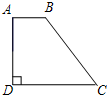如图，在直角梯形ABCD中，AB∥DC，∠D=90°，若AD=8，BC=10，则cosC的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
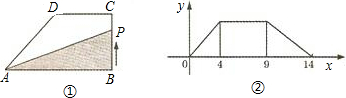
如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，且AB=BC=4AD，E是AB上的一点，DE⊥EC．求证：CE平分∠BCD．
如图，在直角梯形ABCD中，∠A=∠B=90°，∠C=45°，AB=4，AD=5，把梯形沿过点D的直线折叠，使点A刚好落在BC边上，则此时折痕的长为
如图，在直角梯形ABCD中，若AD=5，点A的坐标为（-2，7），则点D的坐标为（ ）